Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(\omega=2\pi f=5\pi\) ; A = 4cm
\(\omega=\sqrt{\frac{K}{m}}=\sqrt{\frac{K}{0,1}}\Rightarrow K=25\)
\(\Delta l_o=\frac{mg}{k}=\frac{0,1.10}{25}=4cm\)
Áp dụng CT: \(F_{đh}max=K\left(\Delta l_o+A\right)\) và \(F_{đh}min=k\left(\Delta l_o-A\right)\)
Suy ra, Fmax = 2 N và Fmin = 0 N
Theo mình là đáp án khác.

lực cực đại Fđh = K(đenta l + A )
lực cực tiểu Fđh = K(đenta l - A)
với A= 10 cm và bài ra ta có F max / F min = ( đenta l +10) / (đenta l - 10 ) = 7/3
từ đây => đenta l =25 cm mà đenta l = m*g / K => độ cứng k = m*g/25
mà ta có omega = căn (K/m) =căn (1/25) = 1/5
mà T =2 pi / omega => f = omega / 2pi => tấn số f= 10pi

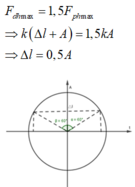
Biểu diễn trên đường tròn lượng giác ta thấy thời gian lò xo nén trong 1 chu kỳ là
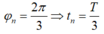
Tỉ số giữa thời gian lò xo giãn và lò xo nén trong một chu kỳ bằng
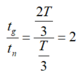
Đáp án D

Kéo vật từ vị trí cân bằng xuống dưới 3cm thì thả vật ra => \(A = 3cm.\)
Hòn bi thực hiện 50 dao động toàn phần trong 20 s
=> Thời gian thực hiện 1 dao động toàn phần (chính là chu kỳ T) : \(T = \frac{20}{50} = 0,4 s.\)
\(\Delta l\) là độ dãn của lò xo khi ở vị trí cân bằng. Tại vị trí cân bằng: \(P = F_{đh}\)
=> \(mg = k\Delta l=> T = 2\pi \sqrt{\frac{m}{k}} = 2\pi\sqrt{\frac{\Delta l}{g}}.\)
=> \(\Delta l = \frac{T^2.g}{4\pi^2} = \frac{T^2}{4} = 0,04 m = 4cm.\)
Lực đàn hồi cực tiểu khác 0 => \(\Delta l \geq A\) => Lực đàn hồi cực tiểu là \(F_{đhmin}=k(\Delta l -A).\)
=> \(\frac{F_{đhmax}}{F_{đhmin}} = \frac{k(\Delta l +A)}{k(\Delta l -A)} = \frac{\Delta l +A}{\Delta l -A} = \frac{4+3}{4-3}= 7.\)

- Lực đạt cực đại khi ở vị trí biên dưới:
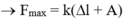
Vì Δl > A nên lực đạt cực tiểu khi vật ở vị trí biên âm:
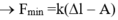
Suy ra:
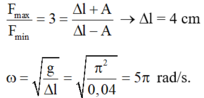



Biên độ dao động: $A = 4cm$
Tỉ số giữa lực đàn hồi cực đại và cực tiểu:
\(\dfrac{F_{max}}{F_{min}}=\dfrac{k(\Delta \ell_0+A)}{k(\Delta\ell_0-A)}=\dfrac{\Delta\ell_0+4}{\Delta\ell_0-4}=2\)
\(\Rightarrow \Delta\ell_0=12cm\)
Tần số dao động:
\(f=\dfrac{\omega}{2\pi}=\dfrac{1}{2\pi}\sqrt{\dfrac{g}{\Delta\ell_0}}=\dfrac{1}{2\pi}\sqrt{\dfrac{10}{0,12}}=1,44(hz)\)