Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử ta chọn hai phân số có cùng tử: và
.
Ta muốn có .
Thế thì a . a = a.(x + y). Từ đó suy ra x + y = a.
Vì vậy với mỗi a > 1 cho trước ta có thể chọn x và y sao cho x + y = a.
Chẳng hạn với a = 11, x = 5, y = 6 ta có:
Mặt khác, Vậy
.
Như vậy ta có thể tìm được vô số cặp phân số mà tổng và tích của chúng bằng nhau.

mình nghĩ là các phân số có tử số là 0 và các mẫu số dương.
VD:0/1 và 0/2......

\(\frac{0}{1}+\frac{0}{1}=0\)
## CHỌN ĐÚNG CHO MÌNH NHEN ヽ(͡◕ ͜ʖ ͡◕)ノヽ(͡◕ ͜ʖ ͡◕)ノヽ(͡◕ ͜ʖ ͡◕)ノ ##

có đó
Khi hai phân số đó có cùng tử số và mẫu số là hai số liên tiếp có tổng bằng tử số

Giả sử ta chọn hai phân số có cùng tử: axax và ayay.
Ta muốn có ax.ay=ax+ay=ay+axxy=a(x+y)xyax.ay=ax+ay=ay+axxy=a(x+y)xy .
Thế thì a . a = a.(x + y). Từ đó suy ra x + y = a.
Vì vậy với mỗi a > 1 cho trước ta có thể chọn x và y sao cho x + y = a.
Chẳng hạn với a = 11, x = 5, y = 6 ta có:
115+116=11.6+11.55.6=12130.115+116=11.6+11.55.6=12130.
Mặt khác, 115.116=11.1130=12130.115.116=11.1130=12130. Vậy 115.116=115+116115.116=115+116.
Như vậy ta có thể tìm được vô số cặp phân số mà tổng và tích của chúng bằng nhau.

Gọi hai cặp phân số tối giản là\(\frac{a}{b}\) và \(\frac{c}{d}\)
Với (a,b) =(c,d)=1. Ta có \(\frac{a}{b}+\frac{c}{d}=\frac{ac}{bd}\Leftrightarrow ad+bc=ac\)
Do ad chia hết cho a nên bc chia hết cho c, mà (b,a)=1 suy ra c chia hết cho a (1)
Tương tự bc chia hết cho a nên ad chia hết cho c mà (d,c) =1 suy ra a chia hết cho c (2)
Từ (1) và(2) suy ra a=c hoặc a=-c
TH1:a=c suy ra b+d =a=c
TH2:a=-c suy ra a=-c=b=-d
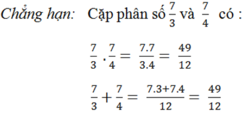
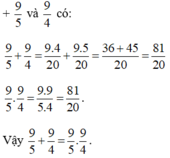
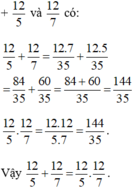
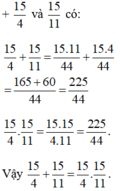

8/5 va 8/3
10/6 và 10/4
Còn nhiều lắm!Chỉ cần hai phân số đó cùng tử và khi cộng mẫu hai phân số lại đc tử của hai số đó là đc!!!!!!!!!!