Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình hoành độ giao điểm:
\(x^2+3x=x+m^2\Leftrightarrow x^2+2x-m^2=0\)
Pt đã cho luôn có 2 nghiệm pb
\(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1x_2=-m^2\end{matrix}\right.\)
Do I là trung điểm đoạn AB \(\Leftrightarrow\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_B}{2}=-1\\y_I=\dfrac{y_A+y_B}{2}=\dfrac{x_A+m^2+x_B+m^2}{2}=m^2-1\end{matrix}\right.\)
Mà I thuộc d'
\(\Leftrightarrow y_I=2x_I+3\Leftrightarrow m^2-1=2.\left(-1\right)+3\)
\(\Leftrightarrow m^2=2\Rightarrow m=\pm\sqrt{2}\)
\(\Rightarrow\sum m^2=4\)

x1 = x2 + 2 (1)
Theo Viet:
x1 + x2 = -2(m - 1) (2)
x1 . x2 = m2 -4m -3 (3)
Từ (1) thay x1 vào (2) ta có:
2.x2 = 2m - 4 => x2 = m - 2
=> x1 = x2 + 2 = m
Thay x1, x2 vào (3) ta có:
m(m - 2) = m2 - 4m -3
=> 2m = -3 => m = -3/2
Thử lại Với m = -3/2 thì y = x2 - 5x + 21/4
Phương trình x2 - 5x + 21/4 = 0 có 2 nghiện là -3/2 và -7/2
x1 = x2 + 2 (1)
Theo Viet:
x1 + x2 = -2(m - 1) (2)
x1 . x2 = m2 -4m -3 (3)
Từ (1) thay x1 vào (2) ta có:
2.x2 = 2m - 4 => x2 = m - 2
=> x1 = x2 + 2 = m
Thay x1, x2 vào (3) ta có:
m(m - 2) = m2 - 4m -3
=> 2m = -3 => m = -3/2
Thử lại Với m = -3/2 thì y = x2 - 5x + 21/4
Phương trình x2 - 5x + 21/4 = 0 có 2 nghiện là -3/2 và -7/2

Pt hoành độ giao điểm:
\(\sqrt{2x^2-2x-m}-x-1=0\)
\(\Leftrightarrow\sqrt{2x^2-2x-m}=x+1\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\2x^2-2x-m=x^2+2x+1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-1\\x^2-4x-1=m\left(1\right)\end{matrix}\right.\)
Bài toán thỏa mãn khi (1) có 2 nghiệm pb \(x\ge-1\)
Từ đồ thị hàm \(y=x^2-4x-1\) ta thấy \(-5< m\le4\)

Phương trình hoành độ giao điểm: x 2 − 2 x − 2 = x + m ⇔ x 2 − 3 x − 2 − m = 0
(d) cắt (P) tại hai điểm phân biệt A, B ⇔ Δ > 0 ⇔ 17 + 4 m > 0 ⇔ m > − 17 4
Giả sử (*) có hai nghiệm x 1 , x 2 thì x 1 + x 2 = − b a = 3 x 1 . x 2 = c a = − m − 2
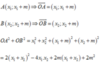
= 18 − 4 ( − 2 − m ) + 6 m + 2 m 2 = 2 m 2 + 10 m + 26 = 2 m + 5 2 2 + 27 2 ≥ 27 2 với m > − 17 4
Vậy giá trị nhỏ nhất của O A 2 + O B 2 là 27 2 khi m = − 5 2
Đáp án cần chọn là: A