Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

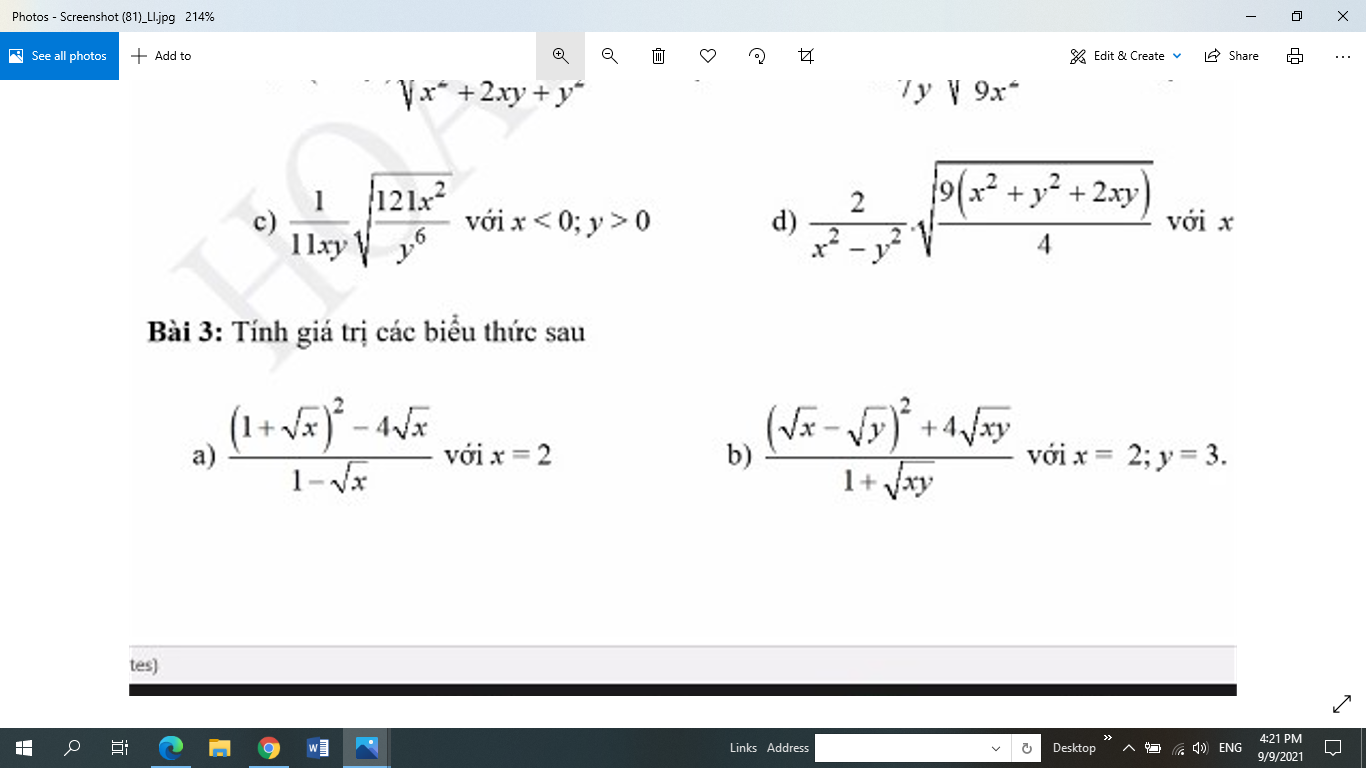
\(3,\\ a,\dfrac{\left(1+\sqrt{x}\right)^2-4\sqrt{x}}{1-\sqrt{x}}\\ =\dfrac{\sqrt{x}-2\sqrt{x}+1}{1-\sqrt{x}}=\dfrac{\left(1-\sqrt{x}\right)^2}{1-\sqrt{x}}=1-\sqrt{x}=1-\sqrt{2}\)
\(b,\dfrac{\left(\sqrt{x}-\sqrt{y}\right)^2+4\sqrt{xy}}{1+\sqrt{xy}}\\ =\dfrac{x+2\sqrt{xy}+y}{1+\sqrt{xy}}=\dfrac{\left(\sqrt{x}+\sqrt{y}\right)^2}{1+\sqrt{xy}}\\ =\dfrac{\left(\sqrt{2}+\sqrt{3}\right)^2}{1+\sqrt{6}}=\dfrac{5+2\sqrt{6}}{1+\sqrt{6}}\\ =\dfrac{\left(5+2\sqrt{6}\right)\left(\sqrt{6}-1\right)}{5}\\ =\dfrac{3\sqrt{6}+7}{5}\)

Bài 3:
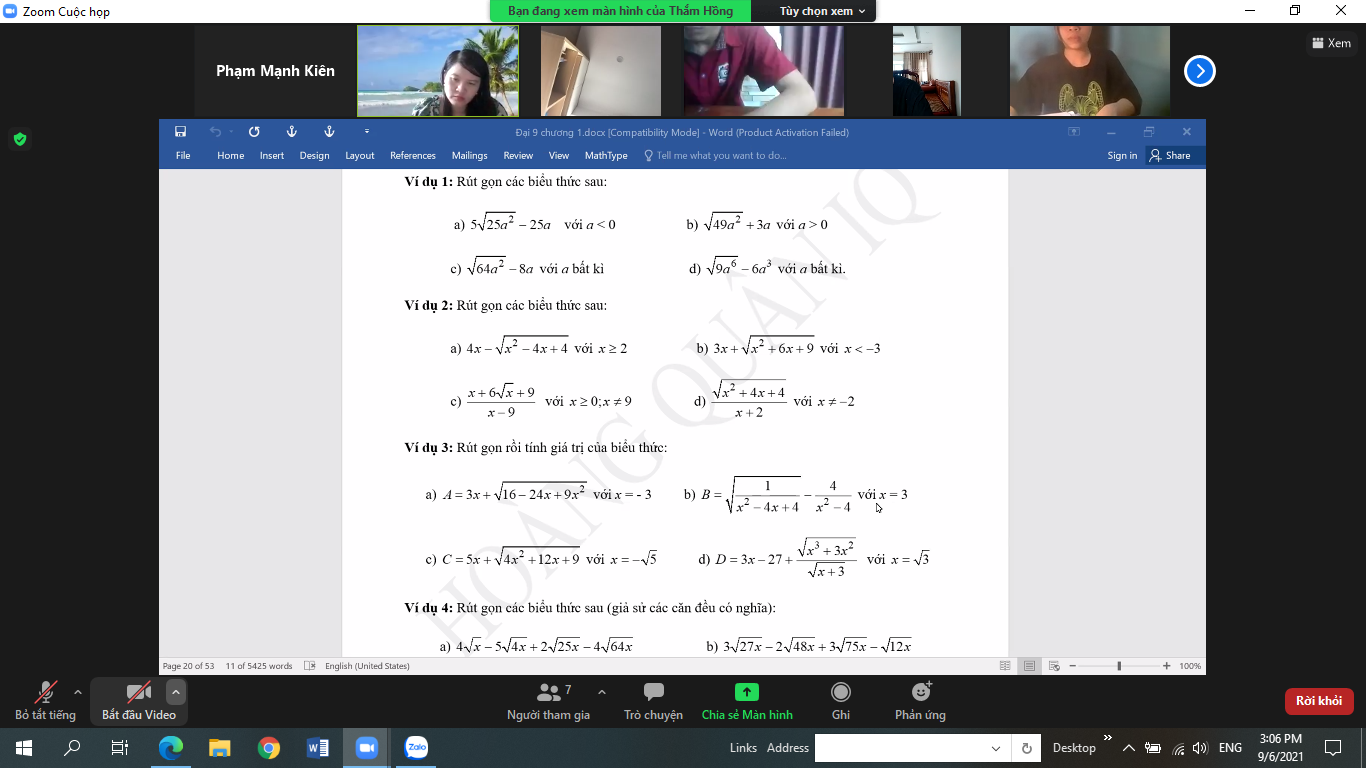
\(a,=\sqrt[3]{\left(x-1\right)^3}-\sqrt[3]{\left(5x+1\right)^3}=x-1-5x-1=-4x-2\\ b,=6a-6a+20a=20a\)
Bài 2:
\(a,=2\sqrt[3]{6}+3\sqrt[3]{5}-4\sqrt[3]{6}-2\sqrt[3]{5}=\sqrt[3]{5}-2\sqrt[3]{6}\\ b,=\sqrt[3]{8}-4\sqrt[3]{27}+2\sqrt[3]{64}=2-12+16=6\\ c,=\sqrt[3]{64}+\sqrt[3]{48}+\sqrt[3]{36}-\sqrt[3]{48}-\sqrt[3]{36}-\sqrt[3]{27}=4-3=1\\ d,=\sqrt[3]{162\left(-2\right)\cdot\dfrac{2}{3}}=\sqrt[3]{-216}=-6\)

Bài 3:
a: Ta có: \(C=\dfrac{a^2+\sqrt{a}}{a-\sqrt{a}+1}-\dfrac{2a+\sqrt{a}}{\sqrt{a}}+1\)
\(=a+\sqrt{a}-2\sqrt{a}-1+1\)
\(=a-\sqrt{a}\)
b: Để C=2 thì \(\sqrt{a}-2=0\)
hay a=4

\(4,\\ a,ĐK:x>0;x\ne4;x\ne9\\ B=\dfrac{x+4\sqrt{x}+4-x+4\sqrt{x}-4+4x}{\left(2-\sqrt{x}\right)\left(2+\sqrt{x}\right)}\cdot\dfrac{\sqrt{x}\left(2-\sqrt{x}\right)}{\sqrt{x}-3}\\ B=\dfrac{4\sqrt{x}\left(\sqrt{x}+2\right)}{\left(2-\sqrt{x}\right)\left(2+\sqrt{x}\right)}\cdot\dfrac{\sqrt{x}\left(2-\sqrt{x}\right)}{\sqrt{x}-3}\\ B=\dfrac{4x}{\sqrt{x}-3}\)
\(b,B=1\Leftrightarrow4x=\sqrt{x}-3\Leftrightarrow4x-\sqrt{x}+3=0\\ \Leftrightarrow\left(4x-2\cdot2\cdot\dfrac{1}{4}\sqrt{x}+\dfrac{1}{16}\right)+\dfrac{47}{16}=0\\ \Leftrightarrow\left(2\sqrt{x}-\dfrac{1}{4}\right)^2+\dfrac{47}{16}=0\\ \Leftrightarrow x\in\varnothing\)

\(1,\\ a,=\dfrac{\left(3+2\sqrt{3}\right)\sqrt{3}}{3}+\dfrac{\left(2+\sqrt{2}\right)\left(\sqrt{2}-1\right)}{1}\\ =\dfrac{3\sqrt{3}+6}{3}+\sqrt{2}=\sqrt{3}+1+\sqrt{2}\\ b,=\left(\dfrac{\sqrt{5}+\sqrt{2}}{3}-\dfrac{\sqrt{5}-\sqrt{2}}{3}+1\right)\cdot\dfrac{1}{\left(\sqrt{2}+1\right)^2}\\ =\dfrac{\sqrt{5}+\sqrt{2}-\sqrt{5}+\sqrt{2}+3}{3}\cdot\dfrac{1}{\left(\sqrt{2}+1\right)^2}\\ =\dfrac{2\sqrt{2}+3}{3\left(3+2\sqrt{2}\right)}=\dfrac{1}{3}\)
\(2,\\ A=2x+\sqrt{\left(x-3\right)^2}=2x+\left|x-3\right|\\ =2\left(-5\right)+\left|-5-3\right|=-10+8=-2\\ B=\dfrac{\sqrt{\left(2x+1\right)^2}}{\left(x-4\right)\left(x+4\right)}\left(x-4\right)^2=\dfrac{\left|2x+1\right|\left(x-4\right)}{x+4}\\ B=\dfrac{17\cdot4}{12}=\dfrac{17}{3}\)

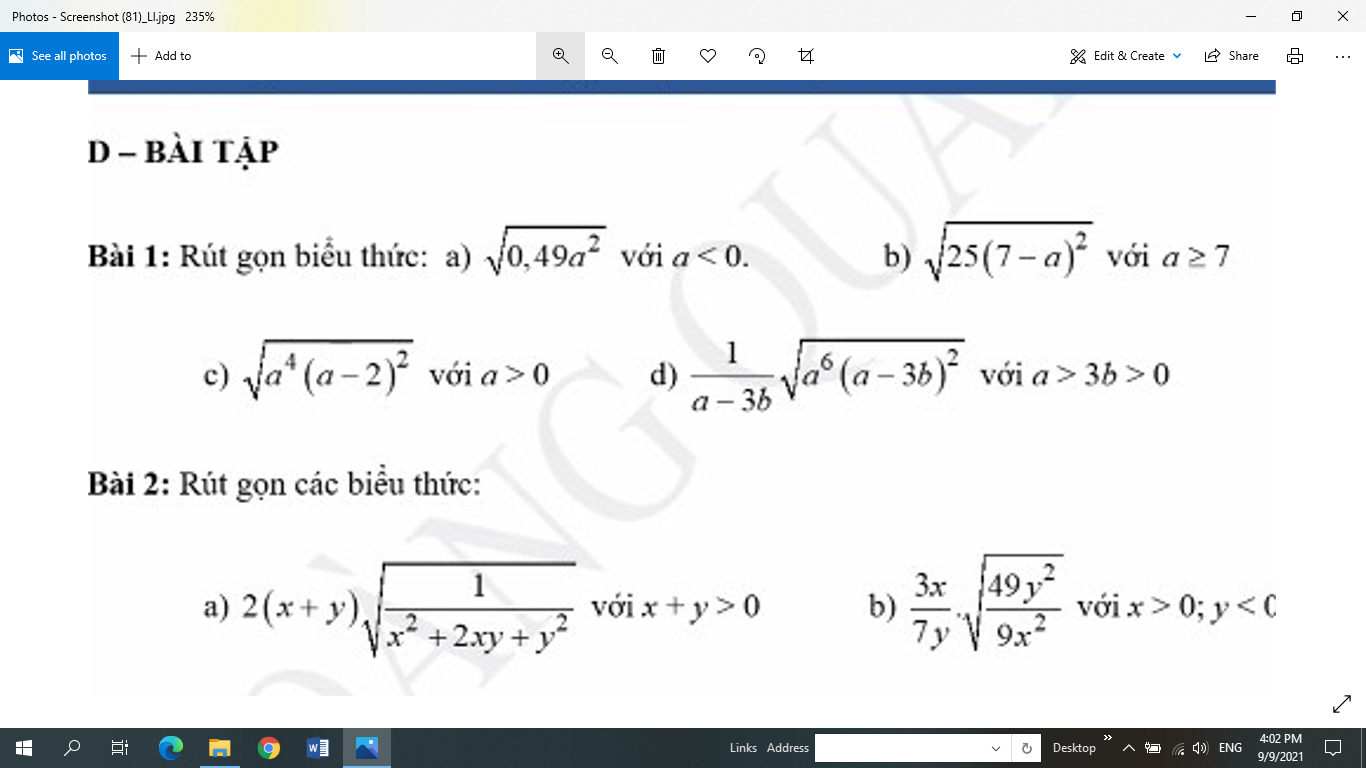
Bài 1:
a: \(\sqrt{0.49a^2}=-0.7a\)
b: \(\sqrt{25\left(a-7\right)^2}=5a-35\)
c: \(\sqrt{a^4\left(a-2\right)^2}=a^2\cdot\left(a-2\right)\)
d: \(\dfrac{1}{a-3b}\cdot\sqrt{a^6\left(a-3b\right)^2}\)
\(=\dfrac{1}{a-3b}\cdot a^3\cdot\left(a-3b\right)=a^3\)
Bài 2:
a: \(2\left(x+y\right)\cdot\sqrt{\dfrac{1}{x^2+2xy+y^2}}\)
\(=2\left(x+y\right)\cdot\dfrac{1}{x+y}\)
=2
b: \(\dfrac{3x}{7y}\cdot\sqrt{\dfrac{49y^2}{9x^2}}\)
\(=\dfrac{3x}{7y}\cdot\dfrac{-7y}{3x}\)
=-1





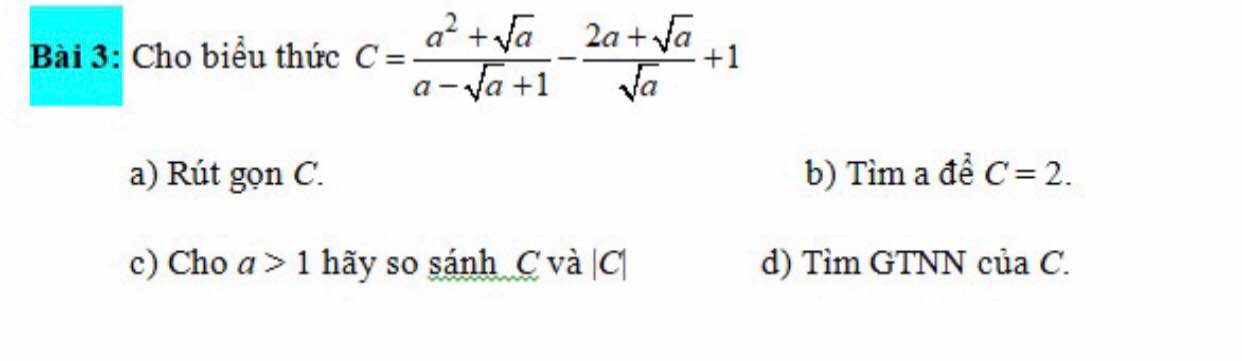
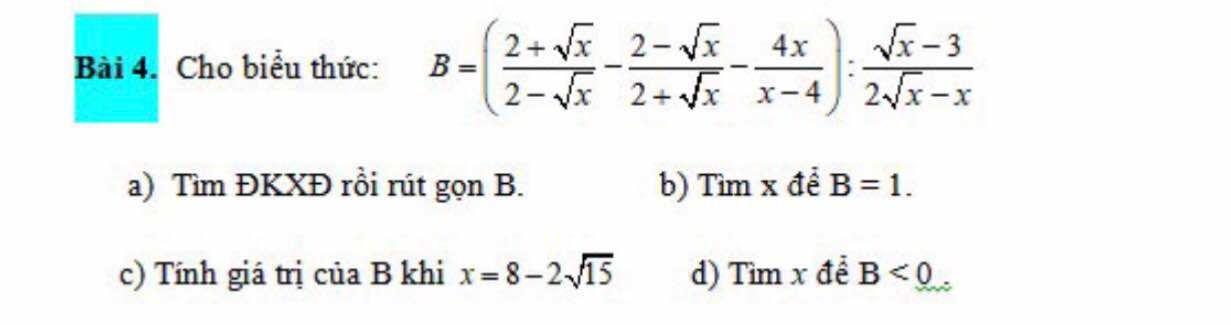



bài 1
\(\widehat{B}=90-\widehat{C}=90-30=60\)
\(sinC=\dfrac{AB}{BC}\Rightarrow BC=\dfrac{AB}{sinC}=\dfrac{30}{sin30}=60\)
áp dụng pytago vào \(\Delta ABC\)
\(AC=\sqrt{BC^2-AB^2}\)=\(\sqrt{60^2-30^2}\)=\(30\sqrt{3}\)=51,96
bài 2
\(\widehat{B}=90-\widehat{C}=90-30=60\)
\(sinC=\dfrac{AB}{BC}\Rightarrow AB=sinC.BC=sin30.5=2,5\)
áp
áp dụng pytago vào \(\Delta ABC\)
\(AC=\sqrt{BC^2-AB^2}=\sqrt{5^2-2,5^2}\)=4,33
bài 3
\(\widehat{E}=90-\widehat{F}=90-47=43\)
\(sinF=\dfrac{ED}{EF}\Rightarrow EF=\dfrac{ED}{sinF}=\dfrac{9}{sin47}=12,31\)
áp dụng pytago vào \(\Delta DEF\)
\(DF=\sqrt{EF^2-ED^2}=\sqrt{12,31^2-9^2}\)=8,4
bài 4
áp dụng pytago vào \(\Delta ABC\)
\(AB=\sqrt{BC^2-AC^2}=\sqrt{32^2-27^2}=17,18\)
\(sinB=\dfrac{AC}{BC}=\dfrac{27}{32}\Rightarrow\widehat{B}=57\)
\(\widehat{C}=90-\widehat{B}=90-57=33\)