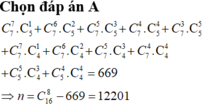T
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HP
14 tháng 9 2021
1.
a, Có \(C_{12}^4=495\) cách chọn 4 viên bi trong 12 viên.
b, Trước hết chọn mỗi màu một viên có \(3.4.5=60\) cách chọn.
Chọn thêm 1 viên trong 9 viên còn lại có 9 cách chọn.
\(\Rightarrow\) Có \(60.9=540\) cách chọn 4 viên bi có đủ 3 màu.
c, Có \(C_3^2\) cách chọn 2 viên bi màu vàng.
Có \(C_{10}^2\) cách chọn 2 viên bi còn lại.
\(\Rightarrow\) Có \(C_3^2.C_{10}^2=135\) cách chọn 4 viên bi có đủ 2 viên màu vàng.
d, Có \(C_4^2\) cách chọn 2 viên bi màu đỏ.
Có \(C_{10}^2\) cách chọn 2 viên bi còn lại.
\(\Rightarrow\) Có \(C_3^2.C_{10}^2=135\) cách chọn 4 viên bi có ít nhất 2 viên bi màu đỏ.
CM
10 tháng 7 2018
Đáp án A
Lấy ngẫu nhiên 3 viên bi trong 12 viên bi có
Gọi X là biến cố “3 bi được chọn có đủ 3 màu”
Lấy 1 viên bi màu đỏ trong 3 bi đỏ có 3 cách.
Lấy 1 viên bi màu xanh trong 4 bi xanh có 4 cách.
Lấy 1 viên bi màu vàng trong 5 bi vàng có 5 cách.
Suy ra số kết quả thuận lợi cho biến cố X là
n(X) = 3.4.5 = 60
HP
10 tháng 7 2021
a, Số cách chọn 6 viên bất kì là \(C_{23}^6=100947\) cách
Số cách chọn 6 viên chỉ màu vàng là \(C_8^6=28\) cách
Số cách chọn 6 viên chỉ màu xanh là \(C_{10}^6=210\) cách
\(\Rightarrow\) có \(100947-28-210=100709\) cách thỏa mãn.
b, Số cách chọn 6 viên có đủ 3 màu là \(5.8.10=400\)
Số cách chọn 6 viên bất kì là \(C_{23}^6=100947\)
\(\Rightarrow\) có \(100947-400=100547\) cách thỏa mãn.
CM
1 tháng 5 2017
Chọn D
Chọn ngẫu nhiên 4 viên bi từ hộp có 12 viên bi thì có 
Số cách lấy để được đủ ba màu là 
Xác suất để 4 viên bi lấy ra có đủ ba màu bằng
HP
27 tháng 12 2021
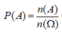
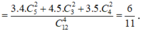
TH1: 4 viên được lấy chỉ gồm 2 màu đỏ và trắng.
\(\Rightarrow\) Có \(C^4_7\) cách chọn.
TH2: 4 viên được lấy chỉ gồm 2 màu đỏ và vàng.
\(\Rightarrow\) Có \(C^4_8\) cách chọn.
TH3: 4 viên được lấy chỉ gồm 2 màu trắng và vàng.
\(\Rightarrow\) Có \(C^4_9\) cách chọn.
TH2 và TH3 đã bao gồm TH lấy 4 viên chỉ có màu trắng và 4 viên chỉ có màu vàng.
\(\Rightarrow\) Có \(C^4_7+C^4_8+C^4_9-C^4_4-C^4_5=225\) cách chọn ra 4 viên bi không đủ ba màu.
CM
23 tháng 5 2017
Sử dụng phương pháp gián tiếp:
Lấy ra 9 viên bi trong 15 viên bi bất kỳ, có C 15 9 cách.
Trường hợp 1: lấy 9 viên bi chỉ có 2 màu là xanh và đỏ, có C 11 9 cách.
Trường hợp 2: lấy 9 viên bi chỉ có 2 màu là xanh và vàng, có C 9 9 cách.
Trường hợp 3: lấy ra 9 viên bi chỉ có màu đỏ và vàng, có C 10 9 cách.
Vậy có : C 15 9 - ( C 11 9 + C 9 9 + C 10 9 ) = 4984 cách.
Chọn C.
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 12 2022
a.
Có \(C_{17}^5\) cách lấy 5 viên bi tùy ý từ 17 viên bi
b.
Lấy 1 bi trắng từ 7 bi trắng, 2 bi xanh từ 4 bi xanh và 2 bi đỏ từ 6 bi đỏ
Số cách lấy là: \(C_7^1.C_4^2.C_6^2\) cách
c.
Các trường hợp thỏa mãn: 1 trắng 1 đỏ 3 xanh, 1 trắng 2 đỏ 2 xanh, 1 trắng 3 đỏ 1 xanh, 2 trắng 1 đỏ 2 xanh, 2 trắng 2 đỏ 1 xanh
Số cách lấy là:
\(C_7^1C_6^1C_4^3+C_7^1C_6^2C_4^2+C_7^1C_6^3C_4^1+C_7^2C_6^1C_4^2+C_7^2C_6^2C_4^1\) cách
21 tháng 12 2022
Thầy có thể giải thích cụ thể hơn về câu a được không thưa thầy?