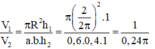Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1.Ta có số hàng phải chuyển tỉ lên nghịch với 36, 45, 60 tức là tỉ lệ thuận với 1/36, 1/45, 1/60 hay là tỉ lệ thuận với 5, 4, 3(nhân 3 phân số với 180). Goij x, y, z là số hàng phải chuyển của các xe I,II,III ta có: x/5=y/4=z/5=(x+y+z)/12=130
Vậy số hàng phải chuyển lần lượt là 650t, 520t, 390t
2.
3.goi x,y lan luot la so hs lop 8a va 8b (x,y>0)
vi tong so 2 lop la 78 nen tco pt1
x+y=78
vi chuyen 2 hs lop 8a sang 8b thj so em trong 2 lop bang nhau nen tco pt2
x-2=y+2 hay x-y=4
=> ta co he pt:
x+y=78
x-y=4
gjaj pt ta dc :
x=41 , y=37
cach 2 ne:
goj x la so hs lop 8a (x>2)
=> so hs lop 8b la:
78-x
vi chuyen 2 hs tu lop 8a sang 8b thj so hs 2 lop bang nhau nen tco pt:
x-2=78-x+2
<=>x+x=78+2+2
<=>2x=82
=> x=41
thay x vao 78-x ta dc so hs lop 8b
4.

Đáp án C
Phương pháp: Lập hàm số chi phí theo một ẩn sau đó tìm giá trị nhỏ nhất của hàm số đó.
Cách giải: Gọi a là chiều dài cạnh đáy hình vuông của hình hộp chữ nhật và b là chiều cao của hình hộp chữ nhật ta có a 2 b = 8 a , b > 0 ⇒ a b = 8 a
Diện tích đáy hình hộp là a 2 và diện tích xung quanh là 4ab nên chi phí để làm thùng tôn là 100 a 2 + 50.4 a b = 100 a 2 + 200 a b = 100 a 2 = 100. 8 a = 100 a 2 + 1600 a = 100 a 2 + 16 a
Áp dụng BĐT Cauchy ta có a 2 + 16 a = a 2 + 8 a + 8 a ≥ 3 a 2 + 8 a + 8 a 3 = 3.4 = 12
Dấu bằng xảy ra khi và chỉ khi a 2 + 8 a ⇔ a = 2.
Vậy chi phí nhỏ nhất bằng 1200000 đồng khi và chỉ khi cạnh đáy hình hộp bằng 2m.

Đổ 8 lít từ thùng một sang thùng hai thì tổng không thay đổi. Vậy:
Số dầu thùng một là :
( 60 : 3 ) + 8 = 28 ( lít )
Số đầu thùng hai là :
60 - 28 = 32 ( lít )
Đáp số : thùng 1 : 28 lít
thùng 2 :32 lít
gọi x là số lít dầu ở thunhf thứ nhất, y là số lít dầu ở thùng thứ 2 ta có:
x+y=60 => x=60-y
Theo đề bài ta có
2(x-8)=(y+8)
=>2(60-y-8)=y+8
<=> 104-2y=y+8
<=> -2y-y=8-104
<=> -3y =-96
<=> y=32
=> x= 60 -y=60-32=28
Vậy thùng 1 có 28 lít dầu
thùng 2 có 32 lít dầu

Số sách trong 5 thùng sách là
5x306=1530 (quyển sách)
Số quyển sách mỗi thư viện được chia là:
1530:9=170 (quyển sách)
Đáp số: 170 quyển sách

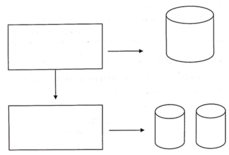
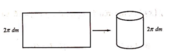
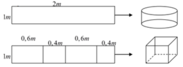
Ban đầu bán kính đáy là R, sau khi cắt và gò ta được 2 khối trụ có bán kính đáy là R 2 . Đường cao của các khối trụ không thay đổi. Ta có:
V 1 = S d h = π . R 2 . h V 2 = 2 S dl . h = 2 π R 2 h = πR 2 h 2
Khi đó: V 1 V 2 = 2
Đáp án C

Đáp án C
Phương pháp
- Gắn hệ trục tọa độ lên mặt thiết diện ngang. Viết phương trình elip.
- Tính diện tích phần thiết diện chỉ chứa dầu.
- Tính thể tích phần dầu trong thùng, sử dụng công thức V = Sh với S là diện tích một phần elip tính được ở trên, h là chiều dài của thùng chứa dầu.
Cách giải:
Chọn hệ trục tọa độ như hình vẽ
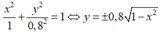
Diện tích thiết diện có chứa dầu là phần diện tích được
gạch chéo trong hình.
Ta tính diện tích phần không gạch chéo S1 là phần hình
phẳng giới hạn bởi đường thẳng y = 0, 4 với một phần elip
phía trên trục hoành có phương trình