
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Xét các tam giác bằng nhau \(\Delta ABC=\Delta A'B'C'\).Kẻ \(AH\perp BC,A'H'\perp B'C'\)(hình bs 16)
Suy ra \(\Delta ABC=\Delta A'B'C'\) nên AC=A'C',\(\widehat{C}=\widehat{C'}\)
Suy ra\(\Delta AHC=\Delta A'H'C'\)(cạnh huyền -góc nhọn) nên AH=A'H'

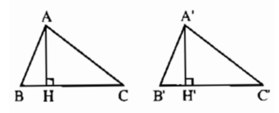
Xét các tam giác bằng nhau ΔABC = ΔA'B'C'. Kẻ AH ⊥ BC, A’H’ ⊥ B’C’
Suy ra ΔABC = ΔA'B'C' nên AC = A’C’, ∠C = ∠C'.
Suy ra ΔAHC = ΔA'H'C' (cạnh – huyền – góc nhọn) nên AH = A’H’.

Gọi đường cao của tam giác ABC là AH;đường cao của tam giác A'B'C' là A'H'
Xét ta được tam giác AHC=tam giác A'H'C'(cạnh huyền- góc nhọn)

theo giả thiết \(\Delta ABC=\Delta EFG\)\(=>\) góc ABH=góc EFI
và AB=EF
có \(\left\{{}\begin{matrix}AH\\EI\end{matrix}\right.\) là các đường phân giác tương ứng
=>góc BAH= góc FEI
xét tam giác ABH và tam giác EFI có:
góc BAH=góc FEI
AB=EF
góc ABH=góc EFI=>tam giác ABH=tam giác EFI(g.c.c)
=>AH=EI(dpcm)

Gọi đường cao của tam giác ABC là AH
Đường cao của tam giác A'B'C là A'H'
Ta xét được: \(\Delta AHC=\Delta A'H'C\)( cạnh huyền góc nhọn )

vì trong 1 tam giác chỉ có 1 đường cao chung
mà 1 cạnh dài,1 cạnh ngắn
nếu cộng thêm đường cao vào vs cạnh dài hơn
và cộng đường cao vào vs cạnh ngắn hơn
thì đương nhiên ta đã ra điều phải chứng minh rùi
mình k giỏi lập luận nên lấy ví dụ cho dẽ hiểu nè:
giả sử đường cao=2cm,cạnh dài=6cm,cạnh ngắn=4cm
tổng đường cao và cạnh dài:2+6=8
tổng đường cao và cạnh ngắn:2+4=6
đều có chung 2,6>4
=>điều phải chứng minh

gọi đường cao của tam giác ABC là AH : đường cao của tam giác A'B'C' là A'H'.
Xét hai tam giác trên ta được tam giác ABC= tam giác A'B'C' (cạnh huyền- góc nhọn)