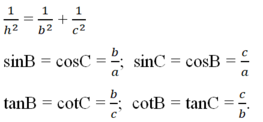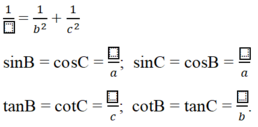Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

chữ " b" mk ghi ở phần b) trước "CMR " là gõ nhầm đấy, ko liên quan j đến bài toán đâu !!

a: \(\Leftrightarrow a^2-4a+4+b^2-6b+9+c^2-2c+1>=0\)
\(\Leftrightarrow\left(a-2\right)^2+\left(b-3\right)^2+\left(c-1\right)^2>=0\)
Dấu '=' xảy ra (a,b,c)=(2;3;1)

Chọn B.
Ta có:
a(a2 – c2) = b(b2 – c2) ⇔ a3 – ac2 = b3 – bc2
⇔ a3 – b3 = ac2 – bc2
⇔ (a – b)(a2 + ab + b2) = c2(a – b)
⇔ a2 + ab + b2 = c2
⇔ ab = c2 – a2 – b2
Ta lại có: 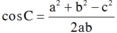
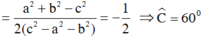

Chọn C.
Theo đầu bài ta có; b(b2 - a2) = c(c2 - a2)
Hay b3 - c3 = a2(b - c)
Mà b - c ≠ 0 nên b2 + bc + c2 = a2
Theo định lí côsin thì a2 = b2 + c2 - 2bccosA
Do đó: b2 + bc + c2 = b2 + c2 - 2bccosA
Suy ra: cos A = - ½ hay góc A bằng 1200.

3. a) \(A=x+\frac{1}{x-1}=x-1+\frac{1}{x-1}+1\ge2\sqrt{\left(x-1\right)\cdot\frac{1}{x-1}}+1=3\)
Dấu "=" \(\Leftrightarrow x-1=\frac{1}{x-1}\Leftrightarrow x=2\)
Min \(A=3\Leftrightarrow x=2\)
b) \(B=\frac{4}{x}+\frac{1}{4y}=\frac{4}{x}+4x+\frac{1}{4y}+4y\cdot-4\left(x+y\right)\)
\(\ge2\sqrt{\frac{4}{x}\cdot4x}+2\sqrt{\frac{1}{4y}\cdot4y}-4\cdot\frac{5}{4}=5\)
Dấu "=" \(\Leftrightarrow\left\{{}\begin{matrix}\frac{4}{x}=4x\\\frac{1}{4y}=4y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=\frac{1}{4}\end{matrix}\right.\)
Min \(B=5\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=\frac{1}{4}\end{matrix}\right.\)
4. Chắc đề là tìm min???
\(C=a+b+\frac{1}{a}+\frac{1}{b}\ge a+b+\frac{4}{a+b}=a+b+\frac{1}{a+b}+\frac{3}{a+b}\)
\(\ge2\sqrt{\left(a+b\right)\cdot\frac{1}{a+b}}+\frac{3}{1}=5\)
Dấu "=" \(\Leftrightarrow\left\{{}\begin{matrix}a=b\\a+b=\frac{1}{a+b}\\a+b=1\end{matrix}\right.\Leftrightarrow a=b=\frac{1}{2}\)
Min \(C=5\Leftrightarrow a=b=\frac{1}{2}\)
1. Áp dụng bđt \(\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}\) ta có:
\(\left(\frac{1}{p-a}+\frac{1}{p-b}\right)+\left(\frac{1}{p-b}+\frac{1}{p-c}\right)+\left(\frac{1}{p-c}+\frac{1}{p-a}\right)\)
\(\ge\frac{4}{2p-a-b}+\frac{4}{2p-b-c}+\frac{4}{2p-a-c}\) \(=\frac{4}{c}+\frac{4}{a}+\frac{4}{b}\)
\(\Rightarrow\frac{1}{p-a}+\frac{1}{p-b}+\frac{1}{p-c}\ge2\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)
Dấu "=" \(\Leftrightarrow a=b=c\)
2. Áp dụng bđt Cauchy ta có :
\(a\sqrt{b-1}=a\sqrt{\left(b-1\right)\cdot1}\le a\cdot\frac{b-1+1}{2}=\frac{ab}{2}\) . Dấu "=" \(\Leftrightarrow b-1=1\Leftrightarrow b=2\)
+ Tương tự : \(b\sqrt{a-1}\le\frac{ab}{2}\). Dấu "=" \(\Leftrightarrow a=2\)
Do đó: \(a\sqrt{b-1}+b\sqrt{a-1}\le ab\). Dấu "=" \(\Leftrightarrow a=b=2\)

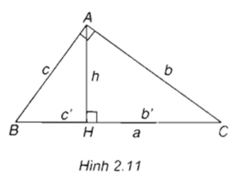
a2 = b2 + c2
b2 = a x b'
c2 = a x c'
h2 = b’ x c'
ah = b x c