Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đặt \(d=\left(n+1,3n+2\right)\).
Suy ra \(\hept{\begin{cases}n+1⋮d\\3n+2⋮d\end{cases}}\Rightarrow3\left(n+1\right)-\left(3n+2\right)=1⋮d\Rightarrow d=1\).
Do đó ta có đpcm.
Đặt \(d=\left(2n+1,4n+3\right)\).
Suy ra \(\hept{\begin{cases}2n+1⋮d\\4n+3⋮d\end{cases}}\Rightarrow\left(4n+3\right)-2\left(2n+1\right)=1⋮d\Rightarrow d=1\).
Do đó ta có đpcm.

Gọi d là ước chung lớn nhất của 3n+1 và 4n+1 (d thuộc N*)
Ta có : 3n+1 chia hết cho d
4n +1 chia hết cho d
==> (4n+1) - (3n+1) chia hết cho d
Hay: n chia hết cho d
==> 3n chia hết cho d
mà 3n+1 chia hết cho d (cmt)
==> (3n+1) - 3n chia hết cho d
Hay: 1 chia hết cho d
mà d thuộc N*
==> d = 1
==> 3n+1 và 4n+1 nguyên tố cùng nhau
==> 3n+1/4n+1 là phân số tối giản. (đpcm)
Gọi d là ƯCLN ( 3n + 1; 4n + 1 )
\(\Rightarrow\)\(3n+1⋮\)d \(\Rightarrow\)\(4.\left(3n+1\right)⋮\)d \(\left(1\right)\)
\(\Rightarrow4n+1⋮\)d \(\Rightarrow\)\(3.\left(4n+1\right)⋮\) d \(\Rightarrow\)\(12n+3⋮\)d \(\left(2\right)\)
Từ \(\left(1\right)\)và \(\left(2\right)\)\(\Rightarrow\)\(\text{[}\left(12n+4\right)-\left(12n+3\right)\text{]}⋮\)d
\(\Rightarrow1⋮\)d \(\Rightarrow\)d = 1
Vì ƯCLN ( 3n + 1 ; 4n + 1 ) = 1 nên \(\frac{3n+1}{4n+1}\)là phân số tối giản

Gọi ƯCLN(14n + 3;24n + 5) = d
=> 14n + 3 ⋮ d => 12(14n + 3) = 168n + 36 ⋮ d
24n + 5 ⋮ d => 7(24n + 5) = 168n + 35 ⋮ d
=> (168n +36) - (168n + 35) ⋮ d
=> 1 ⋮ d => d = 1
Vậy \(\dfrac{14n+3}{24n+5}\) luôn là p/số tối giản với mọi n là số nguyên dương

Ta gọi UWCLN của 2n-1 và 4n+2 là d
Ta có 2n-1 chia het cho d vậy 4n-2 chia hết cho d
4n+2 chia hết cho d vậy 4n+2-4n-2 chia het cho d
Vậy 4 chia hết cho d nên d=1 để 2n-1/4n+2 là tối giản
Vậy 2n-1/4n+2 là tối giản

Mik mới hc lớp 7, mới vửa hc đồng dư nên không biết áp dụng vào đây đúng không nữa
Ta có đồng dư thức như sau:
\(3n\equiv3n\)( mod n) hoặc \(3n\equiv3n\)(mod 3) suy ra \(3n\equiv3n\)(mod 1)
Suy ra: \(3n\equiv3n+1\cdot1\)(mod 1) . r = 0 đó
Vậy ƯCLN(3n;3n+1)=1. Tức 3n và 3n+1 là 2 số nguyên tốcùng nhau. Suy ra \(\frac{3n}{3n+1}\)là phân số tối giản :)

UCLN (3n+5:n+2)=1 thì hai số trên nguyên tố cùng nhau rùi .không rút gon được nữa => tối giản
Gọi d là UCLN ( 3n+5;n+2)
Ta có:\(\hept{\begin{cases}3n+5⋮d\\n+2⋮d\end{cases}}\)
\(n+2⋮d\Rightarrow3\left(n+2\right)\)
hay \(3n+6⋮d\)
ta xét hiệu: \(3n+6-\left(3n+5\right)⋮d\)
\(\Rightarrow1⋮d\)
Vậy P là phân số tối giản với mọi n là STN khi UCLN (3n+5;n+2)=1
Chúc bạn hk tốt!!!

Vì 1/6<1/5;1/7<1/5:1/8<1/5;1/9<1/5
=>1/5+1/6+1/7+1/8+1/9<1/5.2=1(1)
Vậy 1/5+1/6+1/7+1/8+1/9<1
Lại có: 1/10<1/8;1/11<1/8;1/12<1/8;1/13<1/18;1/14<1/8;1/15<1/8;1/16<1/8;1/17<1/8
=>1/10+1/11+1/12+1/13+1/14+1/15+1/16+1/17<1/8.8=1
Vậy 1/10+1/11+1/12+1/13+1/14+1/15+1/16+1/17<1(2)
Từ (1) và (2)
=>1/5+1/6+1/7+...+1/17<2
Vậy 1/5+1/6+1/7+...+1/17<2
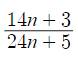
.
Không thể được đâu bạn ơi, giả sử như n = 2, thay vào phân số trên sẽ được kết quả là 8/9 >> không phải là phân số tối giản.
gọi ƯC( 3n+2 và 4n+1) là d
suy ra 3n+2 chia hết cho d và 4n+1 chia hết cho d
suy ra ( 3n+2) - ( 4n +1) chia hết cho d
4(3n+2) - 3(4n+1)chia hết d
12n+8- 12n-3 chia hết d
8-3 chia hết d
5 .............
Vì 3n+2vs 4n+1 là 2 số nguyên tố cung nhau
suy ra d=1
Vậy...............