T
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
0
PT
1
CM
19 tháng 2 2019
Gọi ƯCLN (2m;2m+1)=d
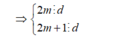
(2m+1) -2m ⋮ d → 1 ⋮ d → d=1
ƯCLN(2m,2m+1) =1
Vậy 2m và 2m+1 là số nguyên tố cùng nhau
TN
2
A
12 tháng 11 2015
GỌi d là ƯC(2m+1,2m)
=>2m chia hết cho d
=>2m+1 chia hết cho d
=> (2m+1)-(2m) chia hết cho d
=>1 chia hết cho d
=> d =1
vậy 2m và 2m+1 là 2 số nguyên tố cùng nhau
AH
Akai Haruma
Giáo viên
18 tháng 11 2023
Bài 1: Gọi hai số lẻ liên tiếp là $2k+1$ và $2k+3$ với $k$ tự nhiên.
Gọi $d=ƯCLN(2k+1, 2k+3)$
$\Rightarrow 2k+1\vdots d; 2k+3\vdots d$
$\Rightarrow (2k+3)-(2k+1)\vdots d$
$\Rightarrow 2\vdots d\Rightarrow d=1$ hoặc $d=2$
Nếu $d=2$ thì $2k+1\vdots 2$ (vô lý vì $2k+1$ là số lẻ)
$\Rightarrow d=1$
Vậy $2k+1,2k+3$ nguyên tố cùng nhau.
Ta có đpcm.
AH
Akai Haruma
Giáo viên
18 tháng 11 2023
Bài 2:
a. Gọi $d=ƯCLN(n+1, n+2)$
$\Rightarrow n+1\vdots d; n+2\vdots d$
$\Rightarrow (n+2)-(n+1)\vdots d$
$\Rightarrow 1\vdots d\Rightarrow d=1$
Vậy $(n+1, n+2)=1$ nên 2 số này nguyên tố cùng nhau.
b.
Gọi $d=ƯCLN(2n+2, 2n+3)$
$\Rightarrow 2n+2\vdots d; 2n+3\vdots d$
$\Rightarrow (2n+3)-(2n+2)\vdots d$ hay $1\vdots d$
$\Rightarrow d=1$.
Vậy $(2n+2, 2n+3)=1$ nên 2 số này nguyên tố cùng nhau.
ND
1
IW
16 tháng 12 2016
Gọi d là ƯCLN(7n+3;2n+1) (d thuộc N*)
Ta có: 7n+3 chia hết cho d => 14n+6 chia hết cho d (1)
2n+1 chia hết cho d => 14n+7 chia hết cho d (2)
TỪ (1) và (2) => 14n+7-14n-6 chia hết cho d
=> 1 chia hết cho d
=> d thuộc Ư(1)={1}
=> d=1
Vì d=1 => ƯCLN(7n+3;2n+1)=1
Vậy 7n+3 và 2n+1 là 2 số nguyên tố cùng nhau ĐPCM
AV
3
4 tháng 12 2016
gọi ucln của n+1 va n+3 là d
nên n+1 chia hết cho d
n+3 chia hết cho d
(n+3)-(n+1) chia hết cho d
2 chia hết cho d =>d=1,2
mà n+1 ko chia hết cho 2 =>d =1
vậy 2 số đó là 2 số nguyên tố cùng nhau
4 tháng 12 2016
đề sai nhé n là số lẻ thì 2 số không nguyên tố cùng nhau
NT
1