Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có 2222 + 4 \(⋮\) 7 => 2222 ≡ - 4 (mod 7) => 22225555 ≡ (- 4)5555(mod 7)
5555 - 4 \(⋮\)7 => 5555 ≡ 4 (mod 7) => 55552222 ≡ 42222 (mod 7)
=> 22225555 + 55552222 ≡ (- 4)5555 + 42222 (mod 7)
Mà 42222 = (-4)2222 => (- 4)5555 + 42222 = (-4)2222. 43333 + 42222
= (-4)2222. 43333 - (- 4)2222 = (-4)2222(43333 - 1) ≡ (43) - 1(mod 7) (1)
Ta lại có : 43 ≡ 1(mod 7) => 43 - 1= 63 7 => 43 - 1 ≡ 0 (mod 7) (2)
Nên (- 4)5555 + 42222 ≡ 0 (mod 7)
Từ (1) và (2) => 22225555 + 55552222 chia hết cho 7.

Tìm x,y biết:
a) 3xy - 5y + 6x = 30
Giải:
3xy - 5y + 6x = 30
<=> y(3x - 5) + (6x - 10) = 20
<=> y(3x - 5) + 2(3x - 5) = 20
<=> (3x - 5)(y + 2) = 20
Ta có bảng sau:
| 3x - 5 | 1 | -1 | 2 | -2 | 4 | -4 | 5 | -5 | 10 | -10 | 20 | -20 |
| y + 2 | 20 | -20 | 10 | -10 | 5 | -5 | 4 | -4 | 2 | -2 | 1 | -1 |
| x | 2 | 43 | 73 | 1 | 3 | 13 | 103 | 0 | 5 | −53 | 253 | -5 |
| y | 0 | -22 | 8 | -12 | 3 | -7 | 2 | -6 | 0 | -4 | -1 | -3 |
Làm theo công thức sách giáo khoa
Bài này làm theo bảnh biển thiên sgk lớp 7:
b) y = - 3x2 + 2x – 1= 
Bảng biến thiên:
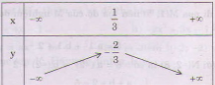
Vẽ đồ thị: - Đỉnh  Trục đối xứng:
Trục đối xứng:  .
.
- Giao điểm với trục tung A(0;- 1).
- Giao điểm với trục hoành: không có.
Ta xác định thêm mấy điểm: B(1;- 2), C(1;- 6). (bạn tự vẽ).
c) y = 4x2 - 4x + 1 =  .
.
còn lại bài bài CMR tham khảo:
https://diendan.hocmai.vn/threads/dong-du-thuc.185712/

b, 5555\(\equiv\)4 (mod 7)=>55552222\(\equiv\)42222 (mod 7)(1)
2222\(\equiv\)3 (mod 7)=>2222=-4 (mod 7)=>22225555\(\equiv\)(-4)5555 (mod 7)(2)
Từ (1) và (2)=>55552222+22225555\(\equiv\)42222+45555 (mod 7)
=>55552222+22225555\(\equiv\)42222 (1-43333) (mod 7)
Ta có:43 \(\equiv\)1 (mod 7)
=>(43)1111\(\equiv\)11111 (mod 7)
=>43333\(\equiv\)1 (mod 7)
=>-43333\(\equiv\)-1(mod 7)
=>1-43333\(\equiv\)0 (mod 7)
=> 55552222+22225555\(\equiv\)0 (mod 7)
Vậy 55552222+22225555\(⋮\)7


Bạn tham khảo tại đây nhé:
Chứng minh 2222^5555+5555^2222 chia hết cho 7 - Nguyễn ...
Chúc bạn học tốt!
ơ thế mình gợi ý bằng không à .-. mình tìm trên mạng rồi mà không có cách đó nên mới nhờ các bạn chứ :vv