Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bạn vẽ hình ra và gọi hai cạnh bên của tam giác cân đó lần lượt là AB, AC.
Gọi E, F lần lượt là trung điểm của các cạnh AB, AC.
Nối E, F với các đỉnh đối diện các cạnh AB, AC ta được 2 tam giac ABF, ACE
Ta có 2 tam giác trên bằng nhau theo trường hợp c.g.c
AB = AC
(Cạnh bên của tam giác cân)
Góc A chung AE = AF => cạnh BF = CE (là 2 đường trung tuyến ứng vói 2 cạnh bên của tam giác cân)
=>Đpcm

Giả sử ∆ABC cân tại A có hai đường trung tuyến BM và CN, ta chứng minh BM = CN
Vì ∆ ABC cân tại A=> AB = AC mà M, N là trung điểm AC, AB nên CM = BN
Do đó ∆CMB ;∆BNC có:
BC chung
CM = BN (cm trên)
AB = AC (∆ABC cân)
=> BM = CN (đpcm)
Giả sử ∆ABC cân tại A có hai đường trung tuyến BM và CN, ta chứng minh BM = CN
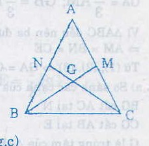
Vì ∆ ABC cân tại A=> AB = AC mà M, N là trung điểm AC, AB nên CM = BN
Do đó ∆CMB ;∆BNC có:
BC chung
CM = BN (cm trên)
AB = AC (∆ABC cân)
=> BM = CN

Giả sử ∆ABC cân tại A có hai đường trung tuyến BM và CN, ta chứng minh BM = CN
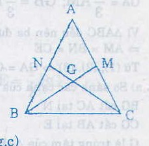
Vì ∆ ABC cân tại A=> AB = AC mà M, N là trung điểm AC, AB nên CM = BN
Do đó ∆CMB ;∆BNC có:
BC chung
CM = BN (cm trên)
AB = AC (∆ABC cân)
=> BM = CN

nếu trong định lí ghi vậy thì chắc chắn điều này luồn đúng, đéo cần chứng minh cũng biết

hình tự vẽ
tam giác cân ABC tại A
=>AB=AC, góc B=góc C
các đường trung tuyến BE và CF (E thuộc AC, F thuộc AB)
Xét tam giác BEC và tam giác CFB
BC chung
góc C= góc B
EC=FB (EC=1/2AC=1/2AB=FB)
=>tam giác BEC=CFB (c.g.c)
=>BE=CF
Vậy trong tam giác cân hai đường trung tuyến ứng với hai cạn bên thì bằng nhau (BE=CF)
Tk mk đi mk học lớp 8 và nằm trong đội tuyển toan lun đó tk đi rồi mk giải cho

A B C E D
-Tam giác ABC cân tại A có BE và CD là 2 đtt
=> AB=AC => AE=AD
Xét tgABE , tgACD có góc A chung , AE=AD,AB=AC
=> ABE=ACD (c g c)
=>BE=CD
-Tam giác ABC có BE và CD là 2 đtt bằng nhau và cắt tại G
=> EG=DG , BG=CG
\(\Delta DGB\),\(\Delta EGC\) có gocDGB = gocEGC ( 2 góc đối đình) EG=DG, BG=CG
=>\(\Delta DGB\)=\(\Delta EGC\)(c.g.c)
=>BD=EC
Xét \(\Delta EBC\) và \(\Delta DCB\) có: BE=CD , BC chung, BD=EC
=>\(\Delta EBC\)=\(\Delta DCB\) (c.c.c)
=>\(\widehat{EBC}=\widehat{DCB}\)
=> TgABC cân tại A (đpcm)