Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Để chứng minh rằng √(a-b) và √(3a+3b+1) là các số chính phương, ta sẽ điều chỉnh phương trình ban đầu để tìm mối liên hệ giữa các biểu thức này. Phương trình ban đầu: 2^(2+a) = 3^(2+b) Ta có thể viết lại phương trình theo dạng: (2^2)^((1/2)+a/2) = (3^2)^((1/2)+b/2) Simplifying the exponents, we get: 4^(1/2)*4^(a/2) = 9^(1/2)*9^(b/2) Taking square roots of both sides, we have: √4*√(4^a) = √9*√(9^b) Simplifying further, we obtain: 22*(√(4^a)) = 32*(√(9^b)) Since (√x)^y is equal to x^(y/), we can rewrite the equation as follows: 22*(4^a)/ = 32*(9^b)/ Now let's examine the expressions inside the square roots: √(a-b) can be written as (√((22*(4^a))/ - (32*(9^b))/)) Similarly, √(3*a + 3*b + ) can be written as (√((22*(4^a))/ + (32*(9^b))/)) We can see that both expressions are in the form of a difference and sum of two squares. Therefore, it follows that both √(a-b) and √(3*a + 3*b + ) are perfect squares.

Có 2a^2 + a = 3b^2 + b
<=> 2a^2 + a - 3b^2 - b = 0
<=> 3a^2 + a - 3b^2 - b = a^2
Xét (a-b).(3a+3b+1) = 3a^2-3ab+3ab-3b^2+a-b = 3a^2-3b^2+a-b = a^2 là 1 số chính phương (1)
Gọi ƯCLN của a-b;3a+3b+1 là d ( d thuộc N sao )
=> a-b chia hết cho d
3a+3b+1 chia hết cho d
a^2 chia hết cho d^2
=> a-b chia hết cho d , 3a+3b +1 chia hết cho d , a chia hết cho d
=> a chia hết cho d , b chia hết cho d , 3a+3b+1 chia hết cho d
=> 1 chia hết cho d => d = 1 ( vì d thuộc N sao )
=> a-b và 3a+3b+1 nguyên tố cùng nhau (2)
Từ (1) và (2) => a-b và 3a+3b+1 đều là số chính phương

1.
\(p=2\Rightarrow p+6=8\) ko phải SNT (ktm)
\(\Rightarrow p>2\Rightarrow p\) lẻ \(\Rightarrow p^2\) lẻ \(\Rightarrow p^2+2021\) luôn là 1 số chẵn lớn hơn 2 \(\Rightarrow\) là hợp số
2.
\(a^2+3a=k^2\Rightarrow4a^2+12a=4k^2\)
\(\Rightarrow4a^2+12a+9=4k^2+9\Rightarrow\left(2a+3\right)^2=\left(2k\right)^2+9\)
\(\Rightarrow\left(2a+3-2k\right)\left(2a+3+2k\right)=9\)
\(\Leftrightarrow...\)

câu 1 bạn phân tích ra là a(a+1)(a+2)(a+3) là 4 số tự nhiên liên tiếp nên chia hết cho 24.
câu 2 bạn phân tích ra thành (a-2)(a-1)a(a+1)(a+2) là 5 số tự nhiên liên tiếp nên chia hết cho 120
bài 3 phân tích ra thành:(a-2)(a-1)a(3a-5) nhưng mình k biết nó chia hết cho 24 ở chỗ nào

https://olm.vn/hoi-dap/detail/92192540983.html
Câu hỏi của La Văn Lết - Toán lớp 8
Bạn tham khảo ở đây nhé
Câu hỏi của La Văn Lết - Toán lớp 8 - Học toán với OnlineMath
Em thma khảo bài làm tại link này nhé!

9a2 + 4b2 = 13ab => (3a)2 + 2.3a.2b + (2b)2 = 25ab => (3a+2b)2 = 25ab => 3a + 2b = 5\(\sqrt{ab}\) (do 3a ; 2b > 0)
9a2 + 4b2 = 13ab => (3a)2 - 2.3a.2b + (2b)2 = ab => (3a- 2b)2 = ab => 3a - 2b = \(\sqrt{ab}\) (ví 3a > 2b > 0)
A = \(\frac{ab}{\left(3a-2b\right)\left(3a+2b\right)}=\frac{ab}{\sqrt{ab}.5\sqrt{ab}}=\frac{1}{5}\)

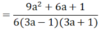
Mình đã làm bài này bằng cách tìm a rồi thế vào M, mong bạn nào có cách giải hay hơn, gọn hơn xin giúp mình. Cảm ơn các bạn!!!