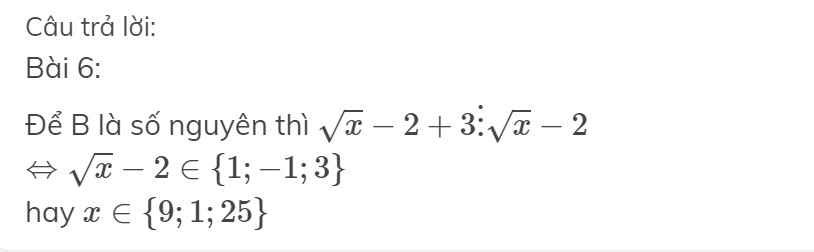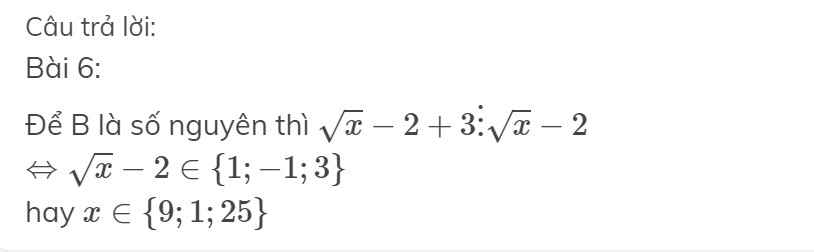Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Với \(a,b>0;a\ne b\)ta có:
\(\left(\sqrt{a}-\sqrt{b}\right)^2>0\Leftrightarrow a-2\sqrt{ab}+b>0\Leftrightarrow2\left(a+b\right)>\left(\sqrt{a}+\sqrt{b}\right)^2\)
\(\Leftrightarrow\sqrt{a}+\sqrt{b}< \sqrt{2\left(a+b\right)}\)
Áp dụng ta được:
\(\sqrt{2}+\sqrt{6}+\sqrt{12}+\sqrt{20}< \sqrt{2\left(2+6\right)}+\sqrt{2\left(12+20\right)}\)
\(=\sqrt{16}+\sqrt{64}=4+8=12\)
Ta có đpcm.

\(\text{a, Ta có:}\)
\(3\sqrt{7}=\sqrt{3^27}=\sqrt{63}\)
\(9=\sqrt{81}\)
\(\text{Vì}:\sqrt{81}>\sqrt{63}\Rightarrow3\sqrt{7}< 9\)
\(\text{b, Vì}\) \(-\sqrt{3}>-\sqrt{5}\Rightarrow-\sqrt{\sqrt{3}}>-\sqrt{\sqrt{5}}\)
\(c,\sqrt{51}-\sqrt{3}\approx5,4>5\)
\(d.\text{Vì}\) \(5>\sqrt{5}\Rightarrow\sqrt{85+5}>\sqrt{85+\sqrt{5}}\)

Bài 6:
Để B là số nguyên thì \(\sqrt{x}-2+3⋮\sqrt{x}-2\)
\(\Leftrightarrow\sqrt{x}-2\in\left\{1;-1;3\right\}\)
hay \(x\in\left\{9;1;25\right\}\)

\(\sqrt{144}.5\sqrt{\frac{16}{9}}+\left|-5\frac{1}{3}\right|\)
\(=12.\frac{20}{3}+-\frac{16}{3}\)
\(=80+-\frac{16}{3}\)
\(=\frac{224}{3}\)
Lần s vt rõ đề hộ con với -.-

A = căn bậc hai của 225 - 1/căn bậc hai của 5 - 1
Tức là :
\(\sqrt{244}\)và \(\sqrt{4}\)
tất nhiên ........
B = căn bậc hai của 196 - 1/căn bậc hai của 6
Tất nhiên ......
2) Tìm GTNN của A = 2 + căn bậc hai của x
\(A=2+\sqrt{x}\)
= \(\sqrt{x+2}\)
3) Tìm GTNN của B = 5 - 2 . căn bậc hai của x - 1
\(B=5-2.\sqrt{x-1}\)
= \(4-2\sqrt{x}\)