K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TN
17 tháng 8 2018
ta có \(x\left(x+1\right)\left(x+2\right)=\left(x^2+x\right)\left(x+2\right)\)
\(=x^3+2x^2+x^2+2x\)
\(=x^3+3x^2+2x\)( đpcm )
học tốt
17 tháng 8 2018
Biến đổi VT ta có :
\(x\left(x+1\right)\left(x+2\right)\)
\(=\left(x^2+x\right)\left(x+2\right)\)
\(=x^3+2x^2+x^2+2x\)
\(=x^3+\left(2x^2+x^2\right)+2x\)
\(=x^3+3x^2+2x=VP\)
Vậy \(x\left(x+1\right)\left(x+2\right)=x^3+3x^2+2x\)
PT
1
PT
1
HN
20 tháng 6 2018
a) \(N=\left(x-5\right)\left(x+2\right)+3\left(x-2\right)\left(x+2\right)-\left(3x-\dfrac{1}{2}x^2\right)+5x^2\)
\(=x^2+2x-5x-10+3x^2-12-3x+\dfrac{1}{2}x^2+5x^2\)
\(=\dfrac{19}{2}x^2-6x-22\)
Vậy biểu thức trên phụ thuộc vào biến x.
b) \(\left(y-1\right)\left(y^2+y+1\right)=y^3-1\)
Giải:
VT = \(\left(y-1\right)\left(y^2+y+1\right)\)
\(=y^3+y^2+y-y^2-y-1\)
\(=y^3-1\)
Vậy \(\left(y-1\right)\left(y^2+y+1\right)=y^3-1\).
HH
20 tháng 6 2018
Giải:
a) \(N=\left(x-5\right)\left(x+2\right)+3\left(x-2\right)\left(x+2\right)-\left(3x-\dfrac{1}{2}x^2\right)+5x^2\)
\(\Leftrightarrow N=x^2-3x-10+3\left(x^2-4\right)-3x+\dfrac{1}{2}x^2+5x^2\)
\(\Leftrightarrow N=x^2-3x-10+3x^2-12x-3x+\dfrac{1}{2}x^2+5x^2\)
\(\Leftrightarrow N=-10-18x+\dfrac{19}{2}x^2\)
Vậy biểu thức trên phụ thuộc vào biễn x
b) \(\left(y-1\right)\left(y^2+y+1\right)\)
\(=y^3-y^2+y^2-y+y-1\)
\(=y^3-\left(y^2-y^2\right)-\left(y-y\right)-1\)
\(=y^3-1\)
Vậy ...
KC
1
20 tháng 11 2021
\(\dfrac{3-x}{3+x}=\dfrac{\left(3-x\right)^2}{\left(3-x\right)\left(3+x\right)}=\dfrac{x^2-6x+9}{9-x^2}\)
LD
2 tháng 1 2019
\(VT=\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}\)
\(=\dfrac{a^2}{ab+ca}+\dfrac{b^2}{ab+bc}+\dfrac{c^2}{ca+bc}\ge\left(Schwarz\right)\dfrac{\left(a+b+c\right)^2}{2\left(ab+bc+ca\right)}\)
Mà theo Cô-si ta có:
\(\left\{{}\begin{matrix}a^2+b^2\ge2ab\\b^2+c^2\ge2bc\\c^2+a^2\ge2ca\end{matrix}\right.\Rightarrow a^2+b^2+c^2\ge ab+bc+ca\)
\(\Rightarrow\left(a+b+c\right)^2\ge3\left(ab+bc+ca\right)\) (hằng đẳng thức)
\(\Rightarrow VT\ge\dfrac{3\left(ab+bc+ca\right)}{2\left(ab+bc+ca\right)}=\dfrac{3}{2}\)
Dấu "=" xảy ra khi a=b=c
3 tháng 9 2017
\(\left(-a-b\right)^2=\left(-a\right)^2-2.\left(-a\right).b+b^2\)
\(=a^2+2ab+b^2\)(1)
\(\left(a+b\right)^2=a^2+2ab+b^2\)(2)
Từ (1) và (2) => \(\left(-a-b\right)^2=\left(a+b\right)^2\)
4 tháng 9 2017
\(\left(-a-b\right)\)\(2\)\(=\)\(\left(-a\right)\)\(2\)\(-\)\(2\)\(.\)\(\left(-a\right)\)\(.\)\(b\)\(+\)\(b^2\)
\(=\)\(a^2\)\(+\)\(2\)\(.\)\(ab\)\(+\)\(b^2\)\(\left(1\right)\)
\(\left(a+b\right)\)\(=\)\(a\)\(+\)\(2\)\(.\)\(ab\)\(+\)\(b\)\(\left(2\right)\)
Từ \(\left(1\right)\)và \(\left(2\right)\)ta có :
\(\left(-a-b\right)\)\(^2\)\(=\)\(\left(a+b\right)\)\(^2\)
NT
0
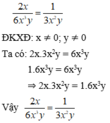
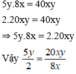
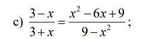
Đề thiếu. Bạn xem lại đề.
Mik viết chx xog mà lỡ tay bấm tạo câu hỏi ạ