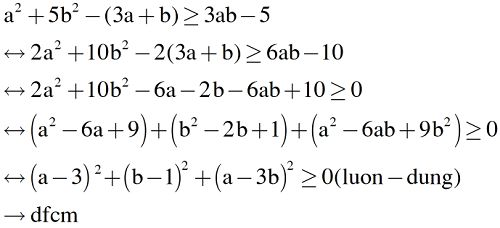K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NT
1
1 tháng 5 2019
a) vì a<b
<=>-5a>-5b
mà 7>2
<=>7-5a>2-5b
b) vì m<n <=>2m<2n<=>2m-5<2n-5
PT
1
HP
2 tháng 8 2016
\(a^2+5b^2-4ab+2a-6b+3\)
\(=a^2-4ab+2a+5b^2-6b+3\)
\(=a^2-2a\left(2b-1\right)+5b^2-6b+3\)
\(=a^2-2.a.\frac{2b-1}{2}+\left(\frac{2b-1}{2}\right)^2+5b^2-6b-\left(\frac{2b-1}{2}\right)^2+3\)
\(=\left(a-\frac{2b-1}{2}\right)^2+5a^2-6b-\frac{\left(2b-1\right)^2}{4}+3\)
\(=\left(a-\frac{2b-1}{2}\right)^2+5a^2-6b-\frac{4b^2-4b+1}{4}+3\)
\(=\left(a-\frac{2b-1}{2}\right)^2+5a^2-6b-b^2+b-\frac{1}{4}+3\)
\(=\left(a-\frac{2b-1}{2}\right)^2+4b^2-5b+\frac{11}{4}\)
\(=\left(a-\frac{2b-1}{2}\right)^2+\left(2b\right)^2-2.2b.\frac{5}{4}+\frac{25}{16}+\frac{19}{16}\)
\(=\left(a-\frac{2b-1}{2}\right)^2+\left(2b-\frac{5}{4}\right)^2+\frac{19}{16}\)
Vì \(\left(a-\frac{2b-1}{2}\right)^2\ge0;\left(2b-\frac{5}{4}\right)^2\ge0=>\left(a-\frac{2b-1}{2}\right)^2+\left(2b-\frac{5}{4}\right)^2+\frac{19}{16}\ge\frac{19}{16}>0\) (với mọi a,b) (đpcm)
T
1
19 tháng 5 2018
Ta có : ( x - 2 )2 \(\ge\)0 \(\Leftrightarrow\)x2 - 4x + 4 \(\ge\)0
\(\Rightarrow\) x2 \(\ge\)4x - 4 \(\Rightarrow\)x2 \(\ge\)4 . ( x - 1 ) \(\Rightarrow\)\(\frac{x^2}{x-1}\)\(\ge\)4
\(\Rightarrow\frac{4a^2}{a-1}+\frac{5b^2}{b-1}+\frac{3c^2}{c-1}\ge4.4+5.4+3.4=48\)
L
1
11 tháng 4 2019
Ta có :
\(a\le b\)
\(\Rightarrow5a\le5b\)
\(\Rightarrow5a-100\le5b-100\)
\(\Rightarrow-5a+100\ge-5b+100\)(đpcm)