
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{2n+1}{8n+4}=\dfrac{2n+1}{4\left(2n+1\right)}=\dfrac{1}{4}\)
Vậy \(\dfrac{2n+1}{8n+4}\) không thể là phân số tối giản

Gọi \(d=ƯC\left(8n+6;2n+1\right)\)
\(\Rightarrow\left\{{}\begin{matrix}8n+6⋮d\\2n+1⋮d\end{matrix}\right.\) \(\Rightarrow8n+6-4\left(2n+1\right)⋮d\)
\(\Rightarrow2⋮d\Rightarrow\left\{{}\begin{matrix}d=1\\d=2\end{matrix}\right.\)
Nhưng do \(2n+1\) lẻ với mọi n nguyên \(\Rightarrow2n+1⋮̸2\) với mọi n nguyên
\(\Rightarrow d\ne2\Rightarrow d=1\) \(\Rightarrow8n+6\) và \(2n+1\) nguyên tố cùng nhau với mọi n nguyên
Hay \(\dfrac{8n+6}{2n+1}\) là phân số tối giản với mọi n nguyên

A = \(\dfrac{2n+1}{8n+6}\) (n \(\ne\) - \(\dfrac{3}{4}\))
Gọi ước chung lớn nhất của 2n + 1 và 8n + 6 là d
Ta có : \(\left\{{}\begin{matrix}2n+1⋮d\\8n+6⋮d\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}8n+4⋮d\\8n+6⋮d\end{matrix}\right.\)
Trừ vế cho vế ta được: 8n + 6 - 8n - 4 ⋮ d ⇒ 2 \(⋮\) d ⇒ d = { 1; 2}
Nếu d = 2 ta có: 2n + 1 ⋮ 2 ⇒ 1 ⋮ 2 ( vô lý)
Vậy d = 1 nên ước chung lớn nhất của 2n + 1 và 8n + 6 là 1
Hay phân số: \(\dfrac{2n+1}{8n+6}\) là phân số tối giản điều phải chứng minh


a: Gọi d=ƯCLN(2n+7;2n+3)
=>2n+7 chia hết cho d và 2n+3 chia hết cho d
=>2n+7-2n-3 chia hết cho d
=>4 chia hết cho d
mà 2n+7 lẻ
nên d=1
=>PSTG
b: Gọi d=ƯCLN(6n+5;8n+7)
=>4(6n+5)-3(8n+7) chia hết cho d
=>-1 chia hết cho d
=>d=1
=>PSTG

a)Gọi ƯCLN(n + 1 ; 2n + 3) = d
\(\Rightarrow\hept{\begin{cases}n+1⋮d\\2n+3⋮d\end{cases}\Rightarrow\hept{\begin{cases}2\left(n+1\right)⋮d\\2n+3⋮d\end{cases}\Rightarrow}\hept{\begin{cases}2n+2⋮d\\2n+3⋮d\end{cases}\Rightarrow}\left(2n+3\right)-\left(2n+2\right)⋮d}\)
\(\Rightarrow\)\(1⋮d\)
\(\Rightarrow d\inƯ\left(1\right)\Rightarrow d\in\left\{\pm1\right\}\)
=> n + 1 ; 2n + 3 là 2 số nguyên tố cùng nhau
\(\Rightarrow\frac{n+1}{2n+3}\)là phân số tối giản
b) Gọi ƯCLN(8n + 5 ; 6n + 4) = d
\(\Rightarrow\hept{\begin{cases}8n+5⋮d\\6n+4⋮d\end{cases}\Rightarrow\hept{\begin{cases}3\left(8n+5\right)⋮d\\4\left(6n+4\right)⋮d\end{cases}\Rightarrow}\hept{\begin{cases}24n+15⋮d\\24n+16⋮d\end{cases}\Rightarrow}\left(24n+16\right)-\left(24n+15\right)⋮d}\)
\(\Rightarrow\)\(1⋮d\)
\(\Rightarrow d\inƯ\left(1\right)\Rightarrow d\in\left\{\pm1\right\}\)
=> 8n + 5 ; 6n + 4 là 2 số nguyên tố cùng nhau
\(\Rightarrow\frac{8n+5}{6n+4}\)là phân số tối giản

Gọi d là ƯCLN(2n-1;8n-3)
ta có 2n-1\(⋮\)d;8n-3\(⋮\)d
=>4*(2n-1)\(⋮\)d;8n-3\(⋮\)d
=>8n-4\(⋮\)d;8n-3\(⋮\)d
=>[(8n-4)-(8n-3)]\(⋮\)d
=>[8n-4-8n+3]\(⋮\)d
=>-1\(⋮\)d
=>d=1
Vì ƯCLN(2n-1;8n-3)=1 nên phân số \(\frac{2n-1}{8n-3}\) luôn tối giản(nEN)
Gọi d là UCLN(2n-1;8n-3)
=>2n-1 chia hết cho d và 8n-3 chia hết cho d
=>4.(2n-1) chia hết cho d và 8n-3 chia hết cho d
=>8n-4 chia hết cho d và 8n-3 chia hết cho d
=>8n-4-8n+3 chia hết cho d
=>-1 chia hết cho d =>d=1
=>điều phải chứng minh

Câu 1:
gọi n-1/n-2 là M.
Để M là phân số tối giản thì ƯCLN (n - 1; n - 2) = 1 hay -1
Theo đề bài: M = n−1n−2n−1n−2 (n ∈∈Zℤ; n ≠2≠2)
Gọi d = ƯCLN (n - 1; n - 2)
=> n - 1 - (n - 2) ⋮⋮d *n - 1 - (n - 2) = n - 1 - n + 2 = n - n + 2 - 1 = 0 + 2 - 1 = 2 - 1 = 1
=> 1 ⋮⋮d
=> d ∈∈Ư (1)
Ư (1) = {1}
=> d = 1
Mà ngay từ lúc đầu d phải bằng 1 rồi.
Vậy nên với mọi n ∈∈Z và n ≠2≠2thì M là phân số tối giản.
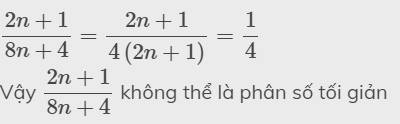
tính ra tui bồi toán tui còn k biết luôn ý :))
mẫu là: 8n + 3 hoặc 8n +5 thì phải chứ em