Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1>chiều dài là:
12:(5-2)x5=20
chiều rộng là:
20-12=8
2> chiều rộng là:
60:5x2=24
chiều dài là:
60-24=36
2> góc 1 là: 180:9x2=40
góc 2 là: 180:9x3=60
góc 3 là: 180-60-40=80
**** cho minh nha
1.
Đáp án:
Chu vi hình chữ nhật là 56m56m
Giải thích các bước giải:
Gọi chiều dài và chiều rộng của hình CN là a;b (m); (a;b > 0)
Theo bài ra ta có :
b2b2 == a5a5 và aa −− bb == 1212
Áp dụng t/c dãy tỉ số = nhau ta có :
a2a2 == b5b5 == a−b5−2a−b5−2 == 123123 == 44
⇒⇒ a2a2 == 44 ⇒⇒ aa == 22 .. 44 == 88 m
và b5b5 == 44 ⇒⇒ bb == 55 .. 44 == 2020 m
Chu vi hình CN là :
(( 88 ++ 2020 )) .. 22 == 5656 (m)
Vậy chu vi hình chữ nhật là 5656 m
2.
Nửa chu vi là:
60 :2=30 (m)60 :2=30 (m)
Theo bài ra:
ab=23ab=23
⇒a=23b⇒a=23b
Ta có:
a+b=30a+b=30
⇒23b+b=30⇒23b+b=30
⇒23b+33b=30⇒23b+33b=30
⇒53b=30⇒53b=30
⇒b=30:53⇒b=30:53
⇒b=18⇒b=18
Nên chiều dài là 18 m18 m và chiều rộng là 30−18=12 m
3.
Gọi số đo ba góc của tam giác ABC lần lượt là A,B,C
Theo đề bài ,ta có:
A/1=B/2=C/3 và A+B+C=180
=>A/1=B/2=C/3=(A+B+C)/(1+2+3)=(A+B+C)/6=180/6=30
Do đó:
+)A/1=30=>A=30
+)B/2=30=>B=60
+)C/3=30=>C=90
Vậy số đo ba góc của tam giác ABC lần lượt là :30,60,90
Vậy tam giác ABC là tam giác vuông
HT

Answer:
Ta gọi chiều cao của ba cạnh là: x, y, z (x, y, z > 0)
Vì chiều cao tỉ lệ nghịch với \(\frac{1}{3};\frac{1}{4};\frac{1}{5}\Rightarrow\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\) và \(x+y+z=70,5\)
Áp dụng tính chất dãy tỉ số bằng nhau
\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{x+y+z}{3+4+5}=\frac{70,5}{12}=\frac{47}{8}\)
\(\Rightarrow\hept{\begin{cases}x=\frac{141}{8}\\y=\frac{47}{2}\\z=\frac{235}{8}\end{cases}}\)

CÔNG THỨC TÍNH CHU VI TAM GIÁC, CÁCH TÍNH CHU VI TAM GIÁC ĐÚNG NHẤT
Công thức tính chu vi tam giác, cách tính chu vi tam giác cũng được phân chia theo cách tính diện tích tam giác cân, vuông, đều. Bởi mỗi dạng tam giác đều có một cách tính chu vi khác nhau.
- Công Thức Tính Chu Vi Tam Giác Thường
Công thức tính chu vi tam giác thường áp dụng cho tất cả các dạng tam giác thường phổ biến với các cạnh thay đổi.
P = A+B+C
Trong đó:
+ a và b và c : Ba cạnh của tam giác thường
- Ví Dụ: Cho một tam giác thường ABC có chiều dài các cạnh lần lượt là 4,5,6 cm. Hỏi diện tích tam giác thường bằng bao nhiêu?
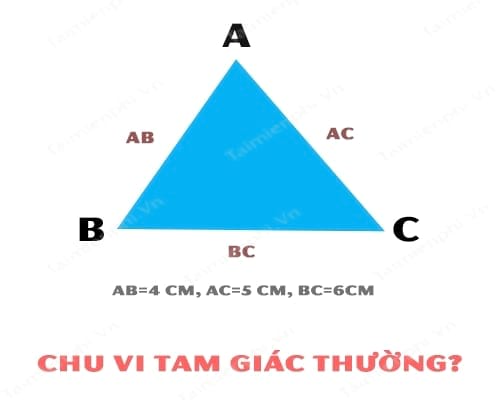
Dựa theo công thức, chúng ta có thể tính chu vi tam giác như sau:
Ta có: a=AB=4 cm, b=AC=5 cm, c=BC=6cm
Suy ra: P = a+b+c = 4 + 5 + 6 = 15 cm
Như vậy chu vi tam giác ABC bằng 15 cm.
- Công Thức Tính Chu Vi Tam Giác Vuông
Công thức tính chu vi tam giác vuông áp dụng cho các dạng tam giác có đường nối vuông góc giữa đỉnh và đáy của một tam giác.
P = A+B+H
Trong đó:
+ a và b : Hai cạnh của tam giác vuông
+ h : chiều cao nối từ đỉnh xuống đáy của một tam giác.
- Ví Dụ: Có một tam giác vuông với chiều dài hai cạnh AC và BC lần lượt là 5 và 6cm. Chiều dài cạnh AB là 7cm. Hỏi chu vi tam giác vuông ABC bằng bao nhiêu.
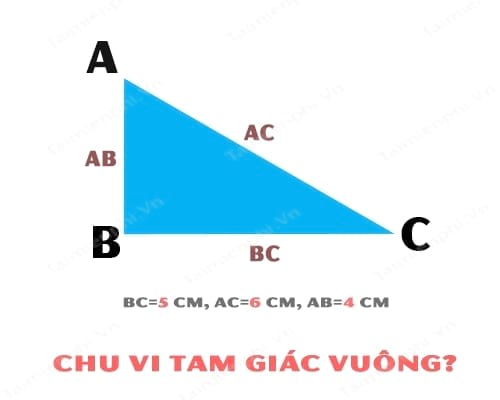
Dựa theo công thức tính chu vi tam giác vuông, ta tính chu vi tam giac vuông như sau:
Ta có: a = AC = 6cm, b = BC = 5cm và h = AB = 4cm
Suy ra P = a+b+h = 6 + 5 + 4 = 15 cm
- Công Thức Tính Chu Vi Tam Giác Cân
Do tam giác cân có ba cạnh bằng nhau và không thay đổi nên cách tính chu vi tam giác cân cũng khá dễ dàng.
P = A X 3
Trong đó:
a là một cạnh bất kỳ trong tam giác cân
- Ví Dụ: Cho một tam giác cân với chiều dài ba cạnh bằng nhau đều bằng 5cm. Hỏi chu vi của tam giác cân này bằng bao nhiêu?
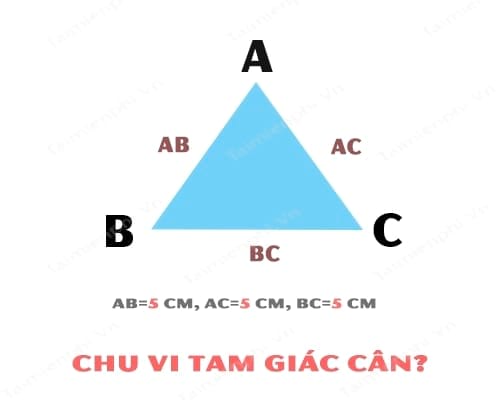
Theo công thức tính chu vi tam giác cân, chúng ta có cách giải như sau:
a = b = c = 5cm
Suy ra: P = ax3 = 5 x 3 = 15 cm
Cách tính chu vi tam giác cân khá dễ phải không?
Đa số công thức tính chu vi tam giác đều được đưa vào phần câu hỏi thêm của nhiều bài toán yêu cầu tính diện tích tam giác bằng công thức tính tam giác có sẵn áp dụng cho cả ba dạng tam giác phổ biến là tam giác thường, vuông. Do đó nếu bạn đã nắm và triển khai đúng các tính diện tích tam giác, bạn có thể áp dụng thêm công thức tính chu vi tam giác để kiếm thêm điểm số hoặc dễ dàng giải quyết vấn đề theo ý muốn.
Nếu bạn phải nhập liệu và tính toán trên Word, việc nắm được cách cách chèn công thức toán học trong Word cũng rất quan trọng bởi cách chèn công thức toán học trong Word khá khác biệt so với việc vẽ và viết trên giấy, người dùng sẽ cần biết cách kết hợp giữa Shape và các chữ để tạo nên một hình ảnh mô tả bài toán đúng cách nhất.
http://thuthuat.taimienphi.vn/cong-thuc-tinh-chu-vi-tam-giac-22867n.aspx
Chúc các bạn thành công!