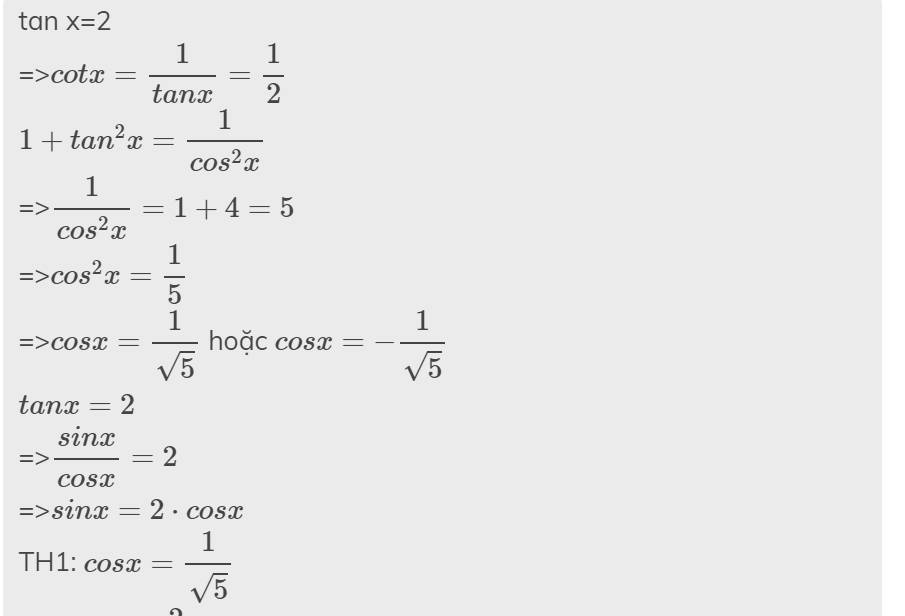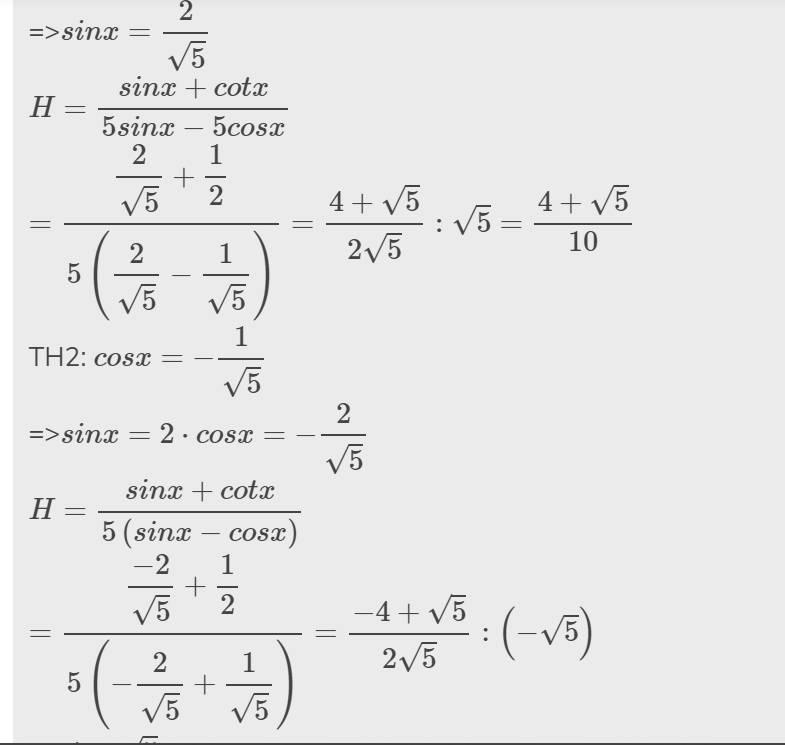Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

cái này là lượng giác ko fai căn thức
công thức cụ thế là sin=đ/h;cos=k/h;tan=đ/k;cot=k/đ
=>đáp án A là đúng

1)
a) trong tam giac ABC vuong tai A co
+)BC2=AB2+AC2
suy ra AC=12cm
+)AH.BC=AB.AC
suy ra AH=7,2cm
b) Trong tu giac AMHN co HMA=HNA=BAC=90 do suy ra AMHN la hcn suy ra AH=MN=7,2cm
suy ra MN=7,2cm
c) goi O la giao diem cu MN va AH
Vi AMHN la hcn (cmt) nen OA=OH=7,2/2=3,6cm
suy ra SBMCN=1/2[OH*(MN+BC)]=39,96cm2
d) Vi AMHN la hcn nen goc AMN=goc HAB
Trong tam giac ABC vuong tai A co AK la dg trung tuyen ung voi canh huyen BC nen AK=BK=KC
suy ra tam giac AKB can tai K
suy ra goc B= goc BAK
Ta co goc B+ goc BAH=90 do
tuong duong BAK+AMN=90 do suy ra AK vuong goc voi MN (dmcm)

A B C H I K M 1
a, muộn rồi nên mk làm qua loa nha!
Dễ cm được AKHI là hình chữ nhật \(\Rightarrow AH=IK\)
Áp dụng hệ thức lượng cho \(\Delta ABC\) \(\Rightarrow IK^2=AH^2=BH.HC\)
b, \(Sin^2B=\left(\dfrac{AC}{BC}\right)^2\) \(=\dfrac{AC^2}{BC^2}\) (1)
theo hệ thức lượng: \(AC^2=HC.BC\)
Thay vào (1)\(\Rightarrow Sin^2B=\dfrac{HC.BC}{BC^2}=\dfrac{HC}{BC}\)

tan x=2
=>\(cotx=\dfrac{1}{tanx}=\dfrac{1}{2}\)
\(1+tan^2x=\dfrac{1}{cos^2x}\)
=>\(\dfrac{1}{cos^2x}=1+4=5\)
=>\(cos^2x=\dfrac{1}{5}\)
=>\(cosx=\dfrac{1}{\sqrt{5}}\) hoặc \(cosx=-\dfrac{1}{\sqrt{5}}\)
\(tanx=2\)
=>\(\dfrac{sinx}{cosx}=2\)
=>\(sinx=2\cdot cosx\)
TH1: \(cosx=\dfrac{1}{\sqrt{5}}\)
=>\(sinx=\dfrac{2}{\sqrt{5}}\)
\(H=\dfrac{sinx+cotx}{5sinx-5cosx}\)
\(=\dfrac{\dfrac{2}{\sqrt{5}}+\dfrac{1}{2}}{5\left(\dfrac{2}{\sqrt{5}}-\dfrac{1}{\sqrt{5}}\right)}=\dfrac{4+\sqrt{5}}{2\sqrt{5}}:\sqrt{5}=\dfrac{4+\sqrt{5}}{10}\)
TH2: \(cosx=-\dfrac{1}{\sqrt{5}}\)
=>\(sinx=2\cdot cosx=-\dfrac{2}{\sqrt{5}}\)
\(H=\dfrac{sinx+cotx}{5\left(sinx-cosx\right)}\)
\(=\dfrac{\dfrac{-2}{\sqrt{5}}+\dfrac{1}{2}}{5\left(-\dfrac{2}{\sqrt{5}}+\dfrac{1}{\sqrt{5}}\right)}=\dfrac{-4+\sqrt{5}}{2\sqrt{5}}:\left(-\sqrt{5}\right)\)
\(=\dfrac{4-\sqrt{5}}{10}\)