Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tham khảo
a) Vì tam giác ABc cân nên :
góc B = góc C
Lại vì AE=Ad => tam giác AED cần
=> Góc E = góc D
Ta có:
góc E + góc D+ góc EAD = Góc B + góc C+ góc BAC(=180 độ)
mà góc EAD = góc BAC ( đói đỉnh)
=> góc E + góc D = góc B+ góc C
mặt khác :góc B = góc C , Góc E = góc D
=> Góc E= góc C mà 2 góc này ơ vị trí so le trong nên :ED// BC ( đpcm)
\(\text{Hình bạn tự vẽ nhoa!}\)
\(\text{a)}\Delta ABC\text{ cân tại }A:\)
\(\Rightarrow\widehat{B}=\widehat{C}\)
\(\text{Vì }AD=AE\)
\(\Rightarrow\Delta AED\text{ cân tại A}:\)
\(\Rightarrow\widehat{E}=\widehat{D}\)
\(\text{Ta có:}\widehat{B}+\widehat{C}+\widehat{BAC}=\widehat{E}+\widehat{D}+\widehat{EAD}=180^0\)
\(\text{mà }\widehat{EAD}\text{ và }\widehat{BAC}\text{(đối đỉnh)}\)
\(\Rightarrow\widehat{E}+\widehat{D}=\widehat{B}+\widehat{C}\)
\(\Rightarrow\widehat{E}=\widehat{C}\)
\(\text{mà chúng so le trong}\)
\(\Rightarrow ED=BC\)
\(\text{b)Xét }\Delta EAB\text{ và }\Delta DAC\text{ có:}\)
\(AE=AD\left(gt\right)\)
\(AB=AC\left(cmt\right)\)
\(\widehat{EAB}=\widehat{CAD}\text{(đối đỉnh)}\)
\(\Rightarrow\Delta EAB=\Delta DAC\left(c.g.c\right)\)
\(BE=CD\text{(2 cạnh tương ứng)}\)
\(\text{c)Ta có:}\Delta EAB=\Delta DAC\left(cmt\right)\)
\(\Rightarrow\widehat{AEB}=\widehat{ADC}\)
\(\text{mà }\widehat{AED}=\widehat{ADE}\)
\(\Rightarrow\widehat{AEB}+\widehat{AED}=\widehat{ADC}+\widehat{ADE}\)
\(\text{Xét }\Delta BED\text{ và }\Delta CDE\text{ có:}\)
\(BE=CD\left(cmt\right)\)
\(\widehat{BED}=\widehat{CDE}\left(cmt\right)\)
\(ED\text{ chung}\)
\(\Rightarrow\Delta BED=\Delta CDE\left(c.g.c\right)\)

a: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
=>AD=AE
Xét ΔBHD vuông tại H và ΔCKE vuông tại K có
BD=CE
góc D=góc E
=>ΔBHD=ΔCKE
=>BH=CK
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
BH=CK
=>ΔAHB=ΔAKC
c: Xét ΔABC có AH/AD=AK/AE
nên KH//DE
=>KH//CB

Hình tự vẽ nha
a) Vì tam giác ABC cân tại A
=> ABC = ACB (1)
Ta có ABC + ABD = ACB + ACE ( cùng = 1800 ) (2)
Từ (1) và (2) => ABD = ACE
Xét tam giác ABD và tam giác ACE có :
AB = AC ( gt )
ABD = ACE ( cmt )
BD = CE ( gt )
=> tam giác ABD = tam giác ACE ( c-g-c )
=> D = E
Xét tam giác BHD và tam giác CKE có :
DHB = EKC ( = 900 )
BD = CE ( gt )
D = E ( cmt )
=> tam giác BHD = tam giác CKE ( ch - gn )
=> đpcm
b) Vì tam giác ABD = tam giác ACE ( chứng minh câu a )
=> HAB = KAC ( 2 góc tương ứng )
Xét tam giác AHB và tam giác AKC có :
HAB = KAC ( cmt )
AHB = AKC ( = 900 )
AB = AC ( gt )
=> tam giác AHB = tam giác AKC ( ch - gn )
=> đpcm
c) Nối H với K
Xét tam giác ADE cân tại A ( vì AD = AE )
=> \(\widehat{D}=\frac{180^0-\widehat{DAE}}{2}\left(1\right)\)
Xét tam giác AHK cân tại A ( vì AH = AK )
\(\Rightarrow\widehat{AHK}=\frac{180^0-\widehat{DAE}}{2}\left(2\right)\)
Từ (1) và (2) => D = AHK
mà 1 góc này ở vị trí đồng vị
=> HK // DE hay HK // BC ( đpcm )
Có j lên đây hỏi nha : Group Toán Học

a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: AD=AE
Xét ΔBHD vuông tại H và ΔCKE vuông tại K có
BD=CE
\(\widehat{D}=\widehat{E}\)
Do đó: ΔBHD=ΔCKE
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔAHB=ΔAKC
c: Xét ΔADE có
AH/AD=AK/AE
nên HK//DE
hay HK//BC

a: Xét ΔABD và ΔACE có
AB=AC
ˆABD=ˆACE
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: AD=AE và ˆD=ˆE
Xét ΔHBD vuông tại H và ΔKEC vuông tại K có
BD=CE
ˆD=ˆE
Do đó: ΔHBD=ΔKCE
Suy ra: BH=CK
b: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
ˆHAB=ˆKAC
Do đó: ΔABH=ΔACK
còn c chờ tý
a: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
=>AD=AE
Xét ΔBHD vuông tại H và ΔCKE vuông tại K có
BD=CE
góc D=góc E
=>ΔBHD=ΔCKE
=>BH=CK
b: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
BH=CK
=>ΔAHB=ΔAKC
c: Xet ΔADE có AH/AD=AK/AE
nên HK//DE
=>BC//HK

a: Xét ΔABD và ΔACE có
AB=AC
ˆABD=ACE^
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: AD=AE và ˆD=ˆED^=E^
Xét ΔHBD vuông tại H và ΔKEC vuông tại K có
BD=CE
ˆD=E^
Do đó: ΔHBD=ΔKCE
Suy ra: BH=CK
b: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
ˆHAB=KAC^
Do dó: ΔABH=ΔACK

a,b: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
=>AD=AE và góc D=góc E; góc DAB=góc EAC
Xet ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc HAB=góc KAC
=>ΔAHB=ΔAKC
=>BH=CK
c: Xét ΔADE có AH/AD=AK/AE
nên HK//DE
=>HK//BC

Sửa đề: I là giao của BH và CK
a: Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
KB=HC
=>ΔKBC=ΔHCB
=>góc IBC=góc ICB
=>IB=IC
Xét ΔAIB và ΔAIC có
AI chung
IB=IC
AB=AC
=>ΔAIB=ΔAIC
b: Xét ΔAHI vuông tại H và ΔAKI vuông tại K có
AI chung
AH=AK
=>ΔAHI=ΔAKI
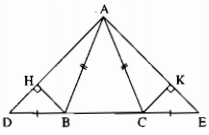
a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
Do đó: ΔABD=ΔACE
Suy ra: \(\widehat{D}=\widehat{E}\) và AD=AE
Xét ΔBHD vuông tại H và ΔCKE vuông tại K có
BD=CE
\(\widehat{D}=\widehat{E}\)
Do đó: ΔBHD=ΔCKE
b: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔABH=ΔACK
Suy ra: AH=AK
c: Xét ΔADE có AH/AD=AK/AE
DO đó: HK//DE
hay BC//HK