Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có P = x2 + 5y2 + 4xy + 6x + 16y + 32
= [(x2 + 4xy + 4y2) + 6x + 12y + 9] + (y2 + 4y + 22) + 19
= [(x + 2y)2 + 2(x + 2y).3 + 32 ] + (y + 2)2 + 19
= (x + 2y + 3)2 + (y + 2)2 + 19
Thấy (x + 2y + 3)2 ≥ 0 với mọi x; y
(y + 2)2 ≥ 0 với mọi y
=> (x + 2y + 3)2 + (y + 2)2 ≥ 0 với mọi x; y
=> (x + 2y + 3)2 + (y + 2)2 + 19 ≥ 19 với mọi x; y
=> P ≥ 19 với mọi x; y
Dấu "=" xảy ra khi x + 2y + 3 = 0 và y + 2 = 0
Bn tự giải tiếp nha, mk ko biết có nhầm chỗ nào ko nhưng cách lm như vậy đó

Lời giải:
$A=5x^2+y^2+4xy-2x-2y+2020$
$=(4x^2+y^2+4xy)+x^2-2x-2y+2020$
$=(2x+y)^2-2(2x+y)+x^2+2x+2020$
$=(2x+y)^2-2(2x+y)+1+(x^2+2x+1)+2018$
$=(2x+y-1)^2+(x+1)^2+2018\geq 2018$
Vậy GTNN của $A$ là $2018$. Giá trị này đạt tại $2x+y-1=0$ và $x+1=0$
Hay $x=-1; y=3$



A = x2 + 5y2 + 4xy + 3x + 8y + 26
= ( x2 + 4xy + 4y2 + 3x + 6y + 9/4 ) + ( y2 + 2y + 1 ) + 91/4
= [ ( x + 2y )2 + 2( x + 2y ).3/2 + (3/2)2 ] + ( y + 1 )2 + 91/4
= ( x + 2y + 3/2 )2 + ( y + 1 )2 + 91/4\(\ge\)91/4
Dấu "=" xảy ra <=>\(\orbr{\begin{cases}\left(x+2y+\frac{3}{2}\right)^2=0\\\left(y+1\right)^2=0\end{cases}}\)<=>\(\orbr{\begin{cases}x+2y=-\frac{3}{2}\\y=-1\end{cases}}\)<=>\(\orbr{\begin{cases}x=\frac{1}{2}\\y=-1\end{cases}}\)
Vậy minA = 91/4 <=>\(\orbr{\begin{cases}x=\frac{1}{2}\\y=-1\end{cases}}\)
A = x2 + 5y2 + 4xy + 3x + 8y + 26
= (x2 + 4xy + 4y2) + (3x + 6y) + 9/4 + (y2 + 2y + 1) + \(\frac{91}{4}\)
= \(\left(x+2y\right)^2+3\left(x+2y\right)+\frac{9}{4}+\left(y+1\right)^2+\frac{91}{4}\)
= \(\left(x+2y+\frac{3}{2}\right)^2+\left(y+1\right)^2+\frac{91}{4}\ge\frac{91}{4}\)
Dấu "=" xảy ra <=> \(\hept{\begin{cases}x+2y+\frac{3}{2}=0\\y+1=0\end{cases}}\Rightarrow\hept{\begin{cases}x+2y=-\frac{3}{2}\\y=-1\end{cases}}\Rightarrow\hept{\begin{cases}x=\frac{1}{2}\\y=-1\end{cases}}\)
Vậy Min A = 91/4 <=> x = 1/2 ; y = -1

\(3=\left(x^2+\frac{1}{x^2}\right)+\left(x^2+\frac{y^2}{4}\right)\ge2+\left|xy\right|\Rightarrow\left|xy\right|\le1\Rightarrow-1\le xy\le1\Rightarrow Bantulmtiep\)
dùng bđt cô si vào phần giả thiết đã cho nhé bạn , mình đang bận không tiện làm . Nếu cần thì tối rảnh mình làm cho

\(A=x^2-x+1\)
\(A=x^2-2\cdot\frac{1}{2}x+\left(\frac{1}{2}\right)^2-\left(\frac{1}{2}\right)^2+1\)
\(A=\left(x-\frac{1}{2}\right)^2-\left(\frac{1}{2}\right)^2+1\)
\(A=\left(x-\frac{1}{2}\right)^2-\frac{1}{4}+1\)
\(A=\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\)
\(\left(x-\frac{1}{2}\right)^2\ge0\Rightarrow\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}\)
\(\Rightarrow GTNNx^2-x-1=\frac{3}{4}\)
với \(\left(x-\frac{1}{2}\right)^2=0;x=\frac{1}{2}\)
\(B=3x^2-2x+1\)
\(B=3\left(x^2-\frac{2}{3}x+\frac{1}{3}\right)\)
\(B=3\left(x^2-2\cdot\frac{1}{3}x+\left(\frac{1}{3}\right)^2-\frac{1}{9}+\frac{1}{3}\right)\)
\(B=3\left[\left(x-\frac{1}{3}\right)^2+\frac{2}{9}\right]\)
\(B=3\left(x-\frac{1}{3}\right)^2+\frac{2}{3}\)
có \(\left(x-\frac{1}{2}\right)^2\ge0\Rightarrow3\left(x-\frac{1}{2}\right)^2+\frac{2}{3}\ge\frac{2}{3}\)
\(\Rightarrow GTNN3x^2-2x+1=\frac{2}{3}\)
với\(\left(x-\frac{1}{2}\right)^2=0;x=\frac{1}{2}\)
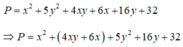
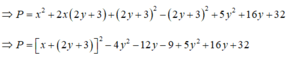
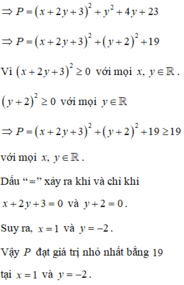
Bạn có ghi nhầm đề không vậy?