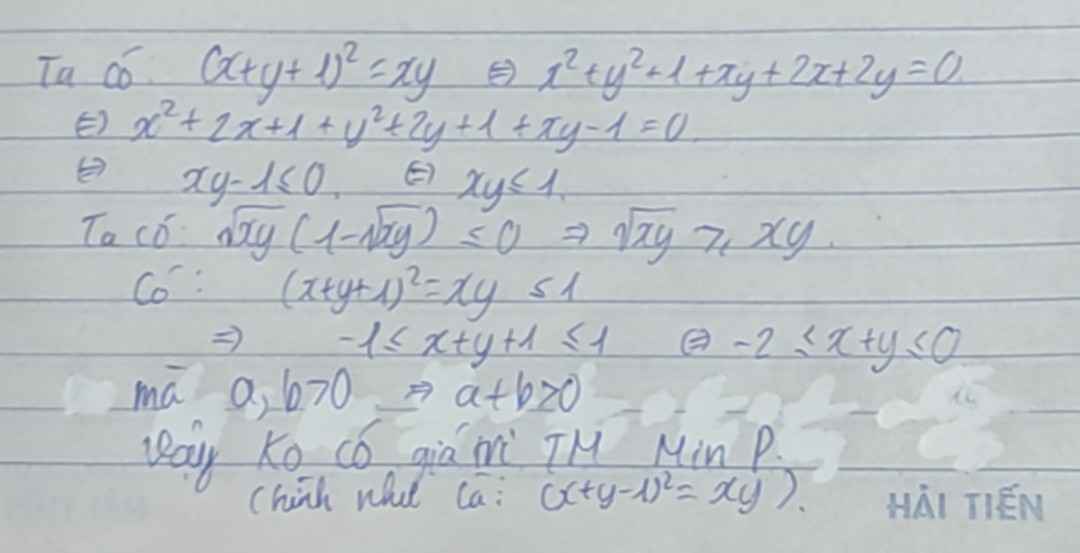Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(A=\frac{1}{x^2+y^2}+\frac{2}{xy}+4xy=\left(\frac{1}{x^2+y^2}+\frac{1}{2xy}\right)+\left(4xy+\frac{1}{4xy}\right)+\frac{5}{4xy}\)
\(\ge\frac{\left(1+1\right)^2}{x^2+2xy+y^2}+2+\frac{5}{\left(x+y\right)^2}=4+2+5=11\)
A = \(\frac{7}{2}\left(\frac{1}{x^2+y^2}+\frac{1}{2xy}\right)+\left(\frac{1}{4xy}+4xy\right)-\frac{5}{2\left(x^2+y^2\right)}\)
Áp dụng bđt cauchy là ra bài

\(1,A=\frac{1}{x^2+y^2}+\frac{1}{xy}=\frac{1}{x^2+y^2}+\frac{1}{2xy}+\frac{1}{2xy}\)
\(\ge\frac{4}{\left(x+y^2\right)}+\frac{1}{\frac{\left(x+y\right)^2}{2}}\ge\frac{4}{1}+\frac{2}{1}=6\)
Dấu "=" <=> x= y = 1/2
\(2,A=\frac{x^2+y^2}{xy}=\frac{x}{y}+\frac{y}{x}=\left(\frac{x}{9y}+\frac{y}{x}\right)+\frac{8x}{9y}\ge2\sqrt{\frac{x}{9y}.\frac{y}{x}}+\frac{8.3y}{9y}\)
\(=2\sqrt{\frac{1}{9}}+\frac{8.3}{9}=\frac{10}{3}\)
Dấu "=" <=> x = 3y

Mình gợi ý để bạn được người khác giúp nhé. Khi đăng bài bạn nên đăng từng câu. Đừng đăng nhiều câu cùng lúc vì nhìn vô không ai muốn giải hết. Giờ bạn tách ra từng câu đăng lại đi. Sẽ có người giúp đấy

Ta có: \(A=\left(\frac{1}{x^2+y^2}+\frac{1}{2xy}\right)+\left(\frac{1}{2xy}+8xy\right)-4xy\ge\frac{\left(1+1\right)^2}{x^2+y^2+2xy}+2\sqrt{\frac{1}{2xy}.8xy}-\left(x+y\right)^2=4+4-1=7\)
Dấu "=" xảy ra khi và chỉ khi x = y = 0,5.

\(A=\frac{1}{x^2+y^2}+\frac{2}{2xy}\ge\frac{\left(1+\sqrt{2}\right)^2}{x^2+y^2+2xy}=\frac{\left(1+\sqrt{2}\right)^2}{\left(x+y\right)^2}=3+2\sqrt{2}\)
Amin =\(3+2\sqrt{2}\) khi x =y =1/2

\(GT\Leftrightarrow x^2+y^2+1+2xy-2x-2y=xy\Leftrightarrow\left(x-1\right)^2+\left(y-1\right)^2=1-xy\rightarrow xy\le1\)
\(\rightarrow\left(x+y-1\right)^2\le1\Leftrightarrow\left(x+y-2\right)\left(x+y\right)\le0\rightarrow x+y\le2\)
\(\text{Ta có:}P=\frac{1}{xy}+\frac{1}{x^2+y^2}+\frac{\sqrt{xy}}{x+y}=\frac{1}{2xy}+\left(\frac{1}{2xy}+\frac{1}{x^2+y^2}\right)+\frac{\left(x+y\right)\sqrt{xy}}{\left(x+y\right)^2}\)
\(\ge\frac{1}{2xy}+\frac{4}{\left(x+y\right)^2}+\frac{2xy}{\left(x+y\right)^2}=\left(\frac{1}{2xy}+\frac{2xy}{\left(x+y\right)^2}\right)+\frac{4}{\left(x+y\right)^2}\)
\(\ge\frac{2}{x+y}+\frac{4}{\left(x+y\right)^2}\ge\frac{2}{2}+\frac{4}{2^2}=2\)
Vậy MinP=2 <=>x=y=1

\(A=\frac{1}{x^2}+\frac{1}{y^2}+\frac{2}{xy}+4xy=\left(\frac{1}{x}+\frac{1}{y}\right)^2+4xy\)
Do x,y\(\ge\)0
Ta có: \(\left(x-y\right)^2\ge0\Rightarrow x^2+y^2\ge2xy\Rightarrow x^2+y^2+2xy\ge4xy\)
\(\Rightarrow\left(x+y\right)^2\ge4xy\Rightarrow\frac{x+y}{xy}\ge\frac{4}{x+y}\Rightarrow\frac{1}{x}+\frac{1}{y}\ge\frac{4}{x+y}\)(*)
Và \(\left(x+y\right)^2\ge4xy\Rightarrow x+y\ge2\sqrt{xy}\)(**)
Áp dụng bất đẳng thức (*) ta có: \(A=\left(\frac{1}{x}+\frac{1}{y}\right)^2+4xy\ge\left(\frac{4}{x+y}\right)^2+4xy=\frac{16}{\left(x+y\right)^2}+4xy\)
Áp dụng bất đẳng thức (**) ta có:\(A\ge\frac{16}{\left(x+y\right)^2}+4xy\ge2\sqrt{\frac{16}{\left(x+y\right)^2}.4xy}=2.\frac{8\sqrt{xy}}{x+y}\ge16\sqrt{xy}\)(do x+y\(\le\)1)
mình đang còn suy nghĩ đây là bản nháp bạn xem thử

Như này nha bạn
Akakakakaka,am,am
ha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihi ha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihi ha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihi ha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihi ha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihi ha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihi ha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihi ha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihi ha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihi ha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihi ha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihi ha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihi ha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihiha ha ha ha hihihihihihihihihihi
\(A=\frac{1}{x^2+y^2}+\frac{2}{xy}+4xy=\left(\frac{1}{x^2+y^2}+\frac{1}{2xy}\right)+\left(4xy+\frac{1}{4xy}\right)+\frac{5}{4xy}\)
\(\ge\frac{4}{\left(x+y\right)^2}+2\sqrt{4xy.\frac{1}{4xy}}+\frac{5}{\left(x+y\right)^2}\)
\(\ge4+2+5=11\)
"=" tại x = y = 1/2