Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sửa đề: A,B,C,D lần lượt là trung điểm của MN,NP,PQ,MQ
Xét ΔNMP có NA/NM=NB/NP
nên AB//MP và BA/MP=NA/NM=1/2
Xét ΔQMP có QC/QP=QD/QM=1/2
nên DC//MP và DC=1/2MP
=>AB//CD và AB=CD
=>ABCD là hình bình hành

1: Xét ΔNMP có NA/NM=NB/NP
nên AB//MP và AB=MP/2
Xét ΔQMP có QC/QP=QD/QM
nên DC//MP và DC=MP/2
=>AB//DC và AB=DC
=>ABCD là hình bình hành

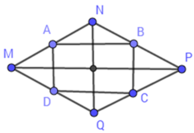
Xét tam giác MNP có: MA = AN; NB = BP (gt) => AB là đường trung bình của tam giác MNP => AB = 1 2 MP; AB // MP (1) (tính chất đường trung bình của tam giác).
Xét tam giác MQP có: MD = DQ; PC = CQ (gt) => CD là đường trung bình của tam giác MQP => CD = 1 2 MP; CD // MP (2) (tính chất đường trung bình của tam giác).
Xét tam giác MNQ có: MA = AN; MD = DQ (gt) => AD là đường trung bình của tam giác MNQ => AD = 1 2 NQ; AD // NQ (tính chất đường trung bình của tam giác).
Từ (1) và (2) suy ra AB = CD; AB // CD => ABCD là hình bình hành (dnnb).
Ta có: AB // MP (cmt); NQ ⊥ MP (gt) => AB ⊥ NQ. Mặt khác AD // NQ (cmt),
suy ra AD ⊥ AB => D A B ^ = 900
Hình bình hành ABCD có D A B ^ = 900nên là hình chữ nhật (dhnb).
Diện tích hình thoi MNPQ là: SMNPQ = 1 2 MP. NQ (3)
Diện tích hình chữ nhật ABCD là:
SABCD = AB. AD = 1 2 MP. 1 2 NQ = 1 4 MP. NQ (4)
Từ (3) và (4) suy ra S A B C D S M N P Q = 1 2 .
Đáp án cần chọn là: A

Xét ΔMQN có
E là trung điểm của MN
H là trung điểm của MQ
Do đó: EH là đường trung bình của ΔMQN
Suy ra: EH//NQ và \(EH=\frac{NQ}{2}\left(1\right)\)
Xét ΔQPN có
F là trung điểm của NP
G là trung điểm của GP
Do đó: FG là đường trung bình của ΔQPN
Suy ra: FG//NQ và\(FG=\frac{NQ}{2}\left(2\right)\)
Từ (1)và (2) suy ra EH//GF và EH=GF
hay EHGF là hình bình hành
Giải
Nối M với P và nối N với Q
Xét tam giác QMP có: \(\left \{ {{\text{H là trung điểm QM (gt)}} \atop {\text{G là trung điểm QP (gt)}}} \right.\)
Do đó HG là đường trung bình của tam giác QMP
\(\Rightarrow HG//MP\left(1\right)\)
Xét tam giác MNP có: \(\left \{ {{\text{E là trung điểm MN (gt)}} \atop {\text{F là trung điểm NP (gt)}}} \right.\)
Do đó EF là đường trung bình của tam giác MNP
\(\Rightarrow EF//MP\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\Rightarrow HG//EF\left(3\right)\)
Xét tam giác MNQ có: \(\left \{ {{\text{H là trung điểm QM (gt)}} \atop {\text{E là trung điểm MN (gt)}}} \right.\)
Do đó HE là đường trung bình của tam giác MNQ
\(\Rightarrow HE//NQ\left(4\right)\)
Xét tam giác NQP có: \(\left \{ {{\text{G là trung điểm QP (gt)}} \atop {\text{F là trung điểm NP (gt)}}} \right.\)
Do đó GF là đường trung bình của tam giác NQP
\(\Rightarrow GF//QN\left(5\right)\)
Từ \(\left(4\right);\left(5\right)\Rightarrow HE//GF\left(6\right)\)
Từ \(\left(3\right);\left(6\right)\Rightarrow\)Tứ giác EFGH là hình bình hành
Vậy tứ giác EFGH là hình bình hành

Xét ΔMQN có
E là trung điểm của MN
H là trung điểm của MQ
Do đó: EH là đường trung bình của ΔMQN
Suy ra: EH//NQ và \(EH=\dfrac{NQ}{2}\left(1\right)\)
Xét ΔQPN có
F là trung điểm của NP
G là trung điểm của GP
Do đó: FG là đường trung bình của ΔQPN
Suy ra: FG//NQ và \(FG=\dfrac{NQ}{2}\left(2\right)\)
Từ (1)và (2) suy ra EH//GF và EH=GF
hay EHGF là hình bình hành

Bài 2:
Xét ΔMQN có
A là trung điểm của MN
D là trung điểm của MQ
Do đó: AD là đường trung bình
=>AD//NQ và AD=NQ/2(1)
Xét ΔNPQ có
B là trung điểm của NP
C là trung điểm của QP
Do đó: BC là đường trung bình
=>BC//NQ và BC=NQ/2(2)
Từ (1) và (2) suy ra AD//BC và AD=BC
hay ABCD là hình bình hành

tự vẽ hình
nối MP
Xét t/g MNP có: AM=AN(gt),BN=BP(gt)
=>AB là đường tb của t/g MNP
=>AB//MP và AB=1/2MP (1)
Xét t/g MQP có: MD=DQ(gt),QC=CP(gt)
=>CD là đường tb của t/g MQP
=.CD//MP và CD=1/2MP(2)
Từ (1) và (2) => AB=CD (3)
Lại có:AB//MP, CD//MP
=>AB//CD (4)
Từ (3)và (4) => tứ giác ABCD là HBH