Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

mik nghĩ câu a.b. bn làm đc,
c,BM=MC(AM là trung tuyến )=>AM c~ là đường cao(đặc biêt của tam giác cân) (1)
xét 2 tam giácvuông BDM và ta giác vuông CDM
MD chung,
MB=MC(trung tuyến AM)
=>2 tam giác vuông BDM=CDM(2 cạnh góc vuông)
=>DM là trung tuyến của BC (2)
từ 1 và 2,ta thấy A,M,D đều thuộc trung tuyến của BC,=>A,M,D thẳng hàng
mik làm sai ở đâu thì nhắc nha

a: Xét ΔABK và ΔHCK có
KA=KH
góc AKB=góc HKC
KB=KC
Do đo: ΔABK=ΔHKC
b: \(BC=\sqrt{8^2+10^2}=2\sqrt{41}\)
\(AK=\dfrac{BC}{2}=\sqrt{41}\)
c: Ta co: ΔEAD vuông tại A
mà AI là đường trung tuyến
nên IA=IE
=>ΔIAE cân tại I
=>\(\widehat{IAE}=\widehat{IEA}\)

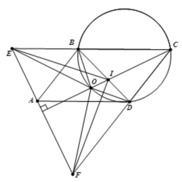
1). Tứ giác OBCD nội tiếp và CO là phân giác góc B C D ^ , suy ra O B D ^ = O C D ^ = O C B ^ = O D B ^ , nên tam giác OBD cân tại O, do đó OB=OD (1).
Tứ giác OBCD nội tiếp O D C ^ = O B E ^ (cùng bù với góc OBC) (2).
Trong tam giác CEF có CO vừa là đường cao vừa là đường phân giác nên tam giác CEF cân tại .
Do A B ∥ C F ⇒ A E B ^ = A F C ^ = E A B ^ , suy ra tam giác ABE cân tại B, nên B E = B A = C D ( 3 )

 .
.
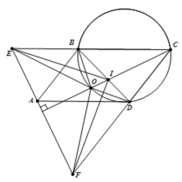
3). Theo trên, ta có B E = C D mà C E = C F ⇒ B C = D F .
Ta có CI là đường phân giác góc BCD, nên I B I D = C B C D = D F B E ⇒ I B . B E = I D . D F .
Mà CO là trung trực EF và I ∈ C O , suy ra IE=IF.
Từ hai đẳng thức trên, suy ra I B . B E . E I = I D . D F . F I .

a: Xét tứ giác BHCD có
M là trung điểm chung của BC và HD
nên BHCD là hình bình hành
c: Xét ΔDHA có MI//HA
nen MI/HA=DM/DH=1/2
=>AH=2MI