K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
14 tháng 2 2018
Tổng bốn góc của 1 tứ giác bằng 360 ° nên: ∠A + ∠ B + ∠ C + ∠ D = 360 °
Suy ra: ∠ A + ∠ B = 360 ° – ( ∠ C + ∠ D) hay
∠ A + ∠ B = 360 ° - 60 ° + 80 ° = 220 °
Mà ∠ A - ∠ B = 10 °
Vậy
∠
A =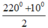 
=
115
°
,
∠
B =
115
°
-
10
°
=
105
°
11 tháng 6 2017
Tứ giác ABCD có: ( ko bik ghi góc nên ko ghi nha )
A + B + C + D = 3600 ( Tổng 4 góc của tứ giác )
A + B = 3600 - ( C + D )
A + B = 3600 - ( 600 + 800 )
A + B = 2200
A = [ ( A + B ) + ( A - B ) ] : 2 = ( 2200 + 100 ) : 2 = 1150
A - B = 100
→ B = A - 100 = 1150 -100 = 1050.
F
28 tháng 8 2020
Bài 1 : Bài giải
Ta có : \(\widehat{A}-\widehat{B}=10^o\text{ }\Rightarrow\text{ }\widehat{A}=\widehat{B}+10^o\)
Trong tứ giác ABCD có :
\(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360^o\)
\(\widehat{B}+10+\widehat{B}+60^o+80^o=360^o\)
\(2\widehat{B}+150^o=360^o\)
\(2\widehat{B}=110^o\)
\(\widehat{B}=55^o\text{ }\Rightarrow\text{ }\widehat{A}=65^o\)
12 tháng 8 2021
\(a,=>\angle\left(B\right)+\angle\left(C\right)=100+80=180^o\)
mà 2 góc ở vị trí trong cùng phía \(=>AB//CD\)
=>ABCD là hình thang
b,\(\dfrac{\angle\left(A\right)}{\angle\left(D\right)}=\dfrac{6}{4}=>\angle\left(A\right)=\dfrac{6\angle\left(D\right)}{4}\)
\(=>\angle\left(A\right)+\angle\left(D\right)=180^o\)(góc trong cùng phía)
\(=>\dfrac{6\angle\left(D\right)}{4}+\angle\left(D\right)=180^o=>\angle\left(D\right)=72^o=>\angle\left(A\right)=\dfrac{6.72^0}{4}=108^o\)
TM
1
LM
25 tháng 8 2016
Ta có: \(\widehat{A}-\widehat{D}=10\Rightarrow\widehat{A}-80=10\Rightarrow\widehat{A}=90\)
Mặt khác: Tổng 4 góc của 1 tứ giác là 360 độ
\(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=360\Rightarrow\widehat{90}+\widehat{B}+60+80=360\Rightarrow\widehat{B}=360-90-60-80\Rightarrow\widehat{B}=130\)
(Mình không biết viết kí hiệu độ nên bạn chịu khó để ý chỗ nào cần thêm kí hiệu độ thì thêm vào nhé)
16 tháng 6 2019
a) Theo bài ra, ta có:
\(\widehat{A}\):\(\widehat{B}\): \(\widehat{C}\) : \(\widehat{D}\) = 1 : 2 : 3 : 4 => \(\frac{\widehat{A}}{1}=\frac{\widehat{B}}{2}=\frac{\widehat{C}}{3}=\widehat{\frac{D}{4}}\) và \(\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}=180^0\)
Áp dụng t/c của dãy tỉ số bằng nhau, ta có:
\(\frac{\widehat{A}}{1}=\widehat{\frac{B}{2}}=\frac{\widehat{C}}{3}=\frac{\widehat{D}}{4}=\frac{\widehat{A}+\widehat{B}+\widehat{C}+\widehat{D}}{1+2+3+4}=\frac{360^0}{10}=36^0\)
=> \(\frac{\widehat{A}}{1}=36^0\) => \(\widehat{A}=36^0\)
\(\widehat{\frac{B}{2}}=36^0\)=> \(\widehat{B}=72^0\)
\(\widehat{\frac{C}{3}}=36^0\) => \(\widehat{C}=108^0\)
\(\widehat{\frac{D}{4}}=36^0\) => \(\widehat{D}=144^0\)
Vậy ...
b) Xét tứ giác ABCD có góc A + góc B + góc C + góc D = 3600
hay góc A + (góc A + 100) + góc C + (góc C + 100) = 3600
=> 2.(góc A + góc C) = 3400
=> góc A + góc C = 1700 => góc B + góc D = 3600 - 1700 = 1900
Ta có: góc B = góc A + 100 (1)
góc C = góc B + 100 (2)
góc D = góc C + 100 (3)
Từ (1) và (2) cộng vế cho vế :
góc B + góc C = góc A + 100 + góc B + 100
=> góc C = góc A + 200 => góc C - A = 200
Mà góc A + góc C = 1700
=> 2. góc C = 1900 => góc C = 950
=> góc A = 950 - 200 = 750
Từ (2) và (3) cộng vế cho vế :
góc C + góc D = góc B + 100 + góc C + 100
=> góc D = góc B + 200 => góc D - góc B = 200
Mà góc D + góc B = 1900
=> 2. góc D = 2100 => góc D = 1050
=> góc B = 1050 - 200 = 850
c) Xét tứ giác ABCD góc A + góc B + góc C + góc D = 3600
=> góc A + góc B = 3600 - góc C - góc D = 3600 - 600 - 800 = 2200
Mà góc A - góc B = 100
=> 2. góc A = 2300 => góc A = 1150
=> góc B = 115 - 100 = 1050
Vậy ...
25 tháng 7 2018
1. Áp dụng định lý tổng 3 góc vào tam giác ICD , bạn tính được góc ICD +góc IDC = 75 độ
Mà góc BCD = 2 góc ICD và góc ADC = 2 góc IDC nên góc BCD + góc ADC = 2.75 = 150 độ
Xét tứ giác ABCD có: góc A + góc B + góc BCD + góc ADC = 360 độ
góc A + 90 độ + 150 độ = 360 độ
góc A = 120 độ
2. góc C của tứ giác là: 180 độ -130 độ = 50 độ
Chúc bạn học tốt.
TT
20 tháng 8 2021
bài 5; tính số đo các góc của tứ giác ABCD biết góc A = 60 độ; góc B = 90 độ. Tính số đo của góc C và góc D:
a, góc C = 100 độ; góc D = 60 độ;
góc A
C, góc B = 80 độ; góc C = 60 độ; 5 góc A = 6 góc D
\(\widehat{A}=110^0\)