Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Hình thang cân ABCD, có:
AB // CD; AD = BC
Xét hình tam giác ACB, có:
I là trung điểm BC (gt)
Q là trung điểm AC (gt)
=> IQ là đường trung bình tam giác ACB
=> IQ // AB
mà AB // CD (cmt)
=> IQ // CD
Xét tam giác ACD, có:
Q là trung điểm AC 9gt)
P là trung điểm CD (gt)
=> QP là đường trung bình tam giác ACD
=> QP = 1/2 AD
mà AD = BC (I là trung điểm BC)
=> IB = IC = QP
Xét tứ giác QIPC, có:
QI // PC (cmt)
=> tứ giác QIPC là hình thang
có: QP = IC (cmt)
=> tứ giác QIPC là hình thang cân (đpcm)
b) Xét tam giác ABC, có:
QI là đường trung bình tam giác ABC (cmt)
=> tam giác CQI = 1/2 tam giác ABC
=> SQIC = 1/2 SABC
Cmtt: SCPQ = 1/2 SACD
mà mình thấy kì kì cái câu này theo mình là = 1/2 chứ sao = 1/4 (theo mình thôi nha)
c) Xét tam giác ABC, có:
M là trung điểm AB (gt)
Q là trung điểm AC (gt)
=> MQ là đường trung bình
=> MQ // BC
MQ = 1/2 BC
cmtt: MN // AD; MN = 1/2 AD
NP = 1/2; NP // BC
PQ // AD; QP = 1/2 AD
Xét tú giác MNPQ, có:
MQ // NP (cùng // BC)
MN // QP (cùng //AD)
=> MNPQ là hình bình hành
có: MQ = NP = 1/2 BC
=> MNPQ là hình thoi (đpcm)
p/s: có chỗ nào không hiểu thì inb hỏi nha ~

Hi vọng bạn có kiến thức vững về BĐT tam giác nha, mấy bài này toàn BĐT tam giác thoi, mình ko chứng minh lại đâu.
Bài 3:
a) Xét tam giác AOB: \(OB>AB-AO\)
Xét tam giác DOC: \(OD>DC-OC\)
Cộng vế theo vế: \(OB+OD>AB+DC-\left(AO+OC\right)\Leftrightarrow BD>AB+DC-AC\Leftrightarrow BD+AC>AB+DC\)
b) Hoàn toàn tương tự với 2 tam giác AOD và BOC:
\(\Rightarrow\hept{\begin{cases}OD>AD-AO\\OB>BC-OC\end{cases}\Rightarrow BD>AD+BC-AC\Leftrightarrow BD+AC>AD+BC}\)
Bài 4:
a) Từ câu 3 ta có \(\hept{\begin{cases}BD+AC>AB+CD\\BD+AC>AD+BC\end{cases}}\)Cộng vế theo vế:
\(\Rightarrow2\left(BD+AC\right)>AB+BC+CD+DA=P_{ABCD}\Rightarrow BD+AC>\frac{P_{ABCD}}{2}\)
b) Câu này thực ra không cần đề cho trước \(AC< \frac{P_{ABCD}}{2}\)đâu, vì đây là điều hiển nhiên mà
Xét 2 tam giác ABC và ADC: \(\hept{\begin{cases}AC< AB+BC\\AC< AD+DC\end{cases}}\)cộng vế theo vế:
\(\Rightarrow2AC< AB+BC+CD+DA=P_{ABCD}\Rightarrow AC< \frac{P_{ABCD}}{2}\)(1)
Hoàn toàn tương tự với 2 tam giác ABD và CBD \(\Rightarrow BD< \frac{P_{ABCD}}{2}\)(2)
Cộng (1) và (2) vế theo vế: \(AC+BD< P_{ABCD}\)

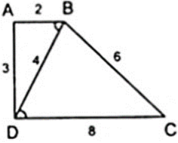
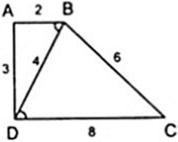
Ta có: Δ BAD ∼ Δ DBC
⇒ A B D ^ = B D C ^ nên AB//CD
⇒ ABCD là hình thang.

Chung minh ABD đồng dạng với BDC
=> \(\widehat{ABD}\)=\(\widehat{BDC}\)
hai góc này ở vị trí sole trong
=> AB//CD