Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

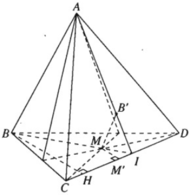
a) MB' qua M và song song với (ABC) và (ABD) ⇒ MB′ song song với giao tuyến AB của hai mặt phẳng này. Ta có: MB′ // AB nên MB' và AB xác định một mặt phẳng. Giả sử MB cắt AB' tại I.
Ta có: I ∈ BM ⇒ I ∈ (BCD)
I ∈ AB′ ⇒ I ∈ (ACD)
Nên I ∈ (BCD) ∩ (ACD) = CD
Có: I ∈ CD
Vậy ba đường thẳng AB', BM và CD đồng quy tại I.
b) MB′ // AB 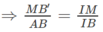
Kẻ MM′ ⊥ CD và BH ⊥ CD
Ta có: MM′ // BH 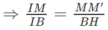
Mặt khác:
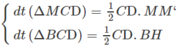
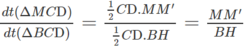
Do đó: 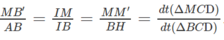
Vậy 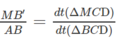
c) Tương tự ta có: 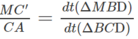
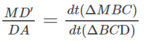
Vậy:
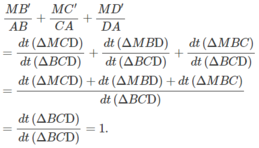

Do ABC cân \(\Rightarrow AM\perp BC\)
Mà \(DA\perp\left(ABC\right)\Rightarrow DA\perp BC\)
\(\Rightarrow BC\perp\left(ADM\right)\Rightarrow BC\perp AH\)
\(\Rightarrow AH\perp\left(BCD\right)\)
b.
Gọi N là trung điểm AB \(\Rightarrow MN\) là đường trung bình tam giác ABC
\(\Rightarrow\left\{{}\begin{matrix}MN||AC\\MN=\dfrac{1}{2}AC=\dfrac{a}{2}\end{matrix}\right.\)
\(\Rightarrow\widehat{\left(AC;DM\right)}=\widehat{\left(MN;DM\right)}=\widehat{DMN}\)
\(DN=\sqrt{AD^2+AN^2}=\sqrt{AD^2+\left(\dfrac{AB}{2}\right)^2}=\dfrac{a\sqrt{89}}{10}\)
\(AM=\sqrt{AB^2-\left(\dfrac{BC}{2}\right)^2}=\dfrac{4a}{5}\Rightarrow DM=\sqrt{AD^2+AM^2}=\dfrac{4a\sqrt{2}}{5}\)
Định lý hàm cos cho tam giác DMN:
\(cos\widehat{DMN}=\dfrac{DM^2+MN^2-DN^2}{2DM.MN}=\dfrac{2\sqrt{2}}{5}\)
\(\Rightarrow\widehat{DMN}\approx55^033'\)
c.
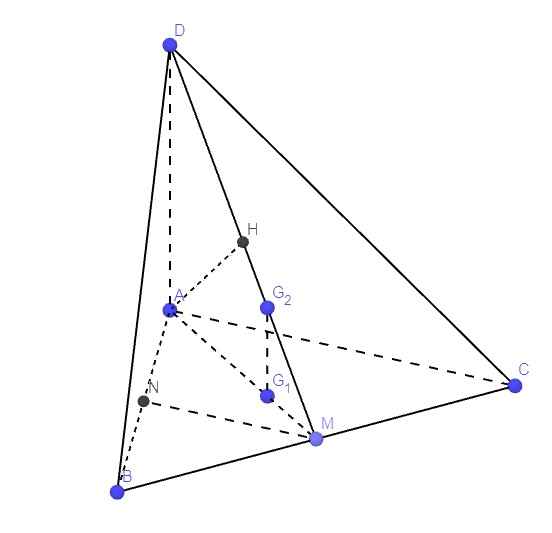
M là trung điểm BC nên hiển nhiên \(G_1\) nằm trên AM và \(G_2\) nằm trên DM
Do \(G_1\) là trọng tâm ABC \(\Rightarrow\dfrac{AG_1}{AM}=\dfrac{2}{3}\Rightarrow\dfrac{MG_1}{AM}=\dfrac{1}{3}\)
Do \(G_2\) là trọng tâm DBC \(\Rightarrow\dfrac{DG_2}{DM}=\dfrac{2}{3}\Rightarrow\dfrac{MG_2}{DM}=\dfrac{1}{3}\)
\(\Rightarrow\dfrac{MG_1}{AM}=\dfrac{MG_2}{DM}\Rightarrow G_1G_2||DA\) (Talet đảo)
Mà \(DA\perp\left(ABC\right)\Rightarrow G_1G_2\perp\left(ABC\right)\)







Trong tam giác ABI, ta có :
\(\dfrac{MB'}{AB}=\dfrac{MI}{BI}\left(1\right)\)