Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

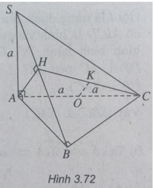
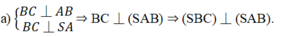
b) AH ⊥ SB mà SB là giao tuyến của hai mặt phẳng vuông góc là (SBC) và (SAB) nên AH ⊥ (SBC).
c) Xét tam giác vuông SAB với đường cao AH ta có:
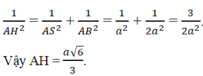
d) Vì OK ⊥ (SBC) mà AH ⊥ (SBC) nên OK // AH, ta có K thuộc CH.
OK = AH/2 = (a√6)/6.

Trong mặt phẳng (SBC), nối HM kéo dài cắt BC tại K \(\Rightarrow AK\in\left(ABC\right)\)
Từ câu a có \(AM\perp\left(SBC\right)\) \(\Rightarrow AM\perp SC\)
Mà \(SC\perp AH\Rightarrow SC\perp\left(AHM\right)\Rightarrow SC\perp AK\) (1)
\(SA\perp\left(ABC\right)\Rightarrow SA\perp AK\) (2)
(1);(2) \(\Rightarrow AK\perp\left(SAC\right)\Rightarrow AK\perp AC\)

a: ta có: BC\(\perp\)AB(ABCD là hình vuông)
BC\(\perp\)SA(SA\(\perp\)(ABCD))
AB,SA cùng thuộc mp(SAB)
Do đó: BC\(\perp\)(SAB)
b: Ta có: BD\(\perp\)AC(ABCD là hình vuông)
BD\(\perp\)SA(SA\(\perp\)(ABCD))
AC,SA cùng thuộc mp(SAC)
Do đó: BD\(\perp\)(SAC)
c: Ta có: BC\(\perp\)(SAB)
AH\(\subset\)(SAB)
Do đó: BC\(\perp\)AH
Ta có: AH\(\perp\)SB
AH\(\perp\)BC
SB,BC cùng thuộc mp(SBC)
Do đó: AH\(\perp\)(SBC)
d: Ta có: AH\(\perp\)(SBC)
SC\(\subset\)(SBC)
Do đó: AH\(\perp\)SC
Ta có: CD\(\perp\)SA(SA\(\perp\)(ABCD))
CD\(\perp\)AD(ABCD là hình vuông)
SA,AD cùng thuộc mp(SAD)
Do đó: CD\(\perp\)(SAD)
=>AK\(\perp\)CD
mà AK\(\perp\)SD
và CD,SD cùng thuộc mp(SCD)
nên AK\(\perp\)(SCD)
=>AK\(\perp\)SC
Ta có: SC\(\perp\)AK
SC\(\perp\)AH
AK,AH cùng thuộc mp(AKH)
Do đó: SC\(\perp\)(AKH)