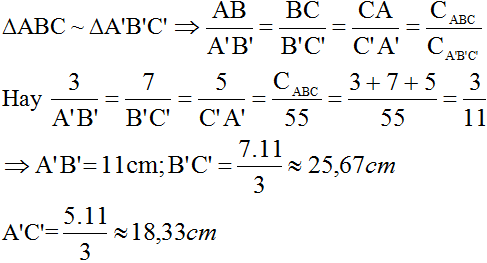Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi x; y; z là độ dài ba cạnh tam giác vuông với z là cạnh huyền thì theo đề bài,ta có:
\(z>y\ge x\ge1\) và
\(\hept{\begin{cases}x^2+y^2=z^2\left(\text{Định lí Pythagoras}\right)\\\frac{xy}{2}=x+y+z\end{cases}}\Leftrightarrow\hept{\begin{cases}\left(x+y\right)^2-2xy=z^2\left(1\right)\\xy=2\left(x+y+z\right)\left(2\right)\end{cases}}\)
Thay (2) lên (1) suy ra \(z^2=\left(x+y\right)^2-4\left(x+y+z\right)\)
\(\Leftrightarrow z^2+4z=\left(x+y\right)^2-4\left(x+y\right)\)
\(\Leftrightarrow z^2+4z+4=\left(x+y\right)^2-4\left(x+y\right)+4\)
\(\Leftrightarrow\left(z+2\right)^2=\left(x+y-2\right)^2\) (*)
Do \(z>y\ge x\ge1\) nên cả hai vế cùng không âm.
Do đó từ (*) suy ra \(z+2=x+y-2\Leftrightarrow z=x+y-4\)
Thay ngược lên (2) và giải tiếp bằng cách phân tích đa thức thành nhân tử và lập bảng xét ước:P.
Note: Em không chắc đâu ạ!
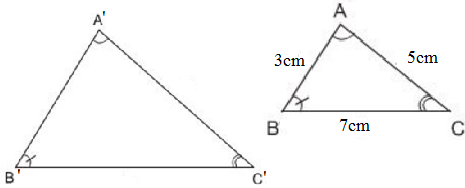
Chu vi tam giác ABC là: AB + BC + CA = 3 + 7 + 5 = 15 (cm)
Δ A’B’C’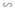 
ΔABC ⇒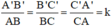 
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
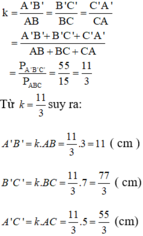
∆ABC ∽ ∆A'B'C' => ABA′B′ABA′B′ = BCB′C′BCB′C′= CAC′A′CAC′A′ = CABCCA′B′C′CABCCA′B′C′
hay 3A′B′3A′B′ = 7B′C′7B′C′ = 5A′C′5A′C′ = CABC55CABC55 = 311311
=> A'B' = 11cm;
B'C' = 7.1137.113 ≈ 25.67 cm
A'C' = 5.1135.113 ≈ 18,33 cm
Chu vi tam giác ABC là 3 + 5 +7 = 15
Ta có :
P ABC / P A'B'C' = AB / A'B'
<=> 15 / 55 = 3 / A'B'
=> A'B' = ( 55 x 3 )/ 15 = 11 cm
P ABC / P A'B'C' = AC / A'C'
<=> 15 / 55 = 5 / A'C'
=> A'C' = ( 55 x 5 ) / 15 = 55/3 cm
P ABC / P A'B'C' = BC / B'C'
<=> 15 / 55 = 7 / B'C'
=> B'C' = ( 55 x 7 ) / 15 = 77/3 cm
A B C A' B' C'
\(\Rightarrow\Delta ABC\)đồng dạng \(\Delta A'B'C'\left(gt\right)\)
Áp dụng tính chất DTSBN , ta có :
\(\frac{AB}{A'B'}=\frac{AC}{A'C'}=\frac{BC}{B'C'}=\frac{AB+AC+BC}{A'B'+A'C'+B'C'}=\frac{C_{ABC}}{C_{A'B'C'}}\)
Hay \(\frac{3}{A'B'}=\frac{7}{B'C'}=\frac{5}{A'C'}=\frac{C_{ABC}}{55}=\frac{3+5+7}{55}=\frac{15}{55}=\frac{3}{11}\)
Với CABC và CA'B'C' lần lượt là chu vi của tam giác ABC , A'B'C'
\(+)\frac{3}{A'B'}=\frac{3}{11}\Rightarrow A'B'=\frac{3.11}{3}=11cm\)
\(+)\frac{7}{A'C'}=\frac{3}{11}\Rightarrow B'C'=\frac{7.11}{3}\approx25,67cm\)
\(+)\frac{5}{A'C'}=\frac{3}{11}\Rightarrow A'C'=\frac{5.11}{3}\approx18,33cm\)