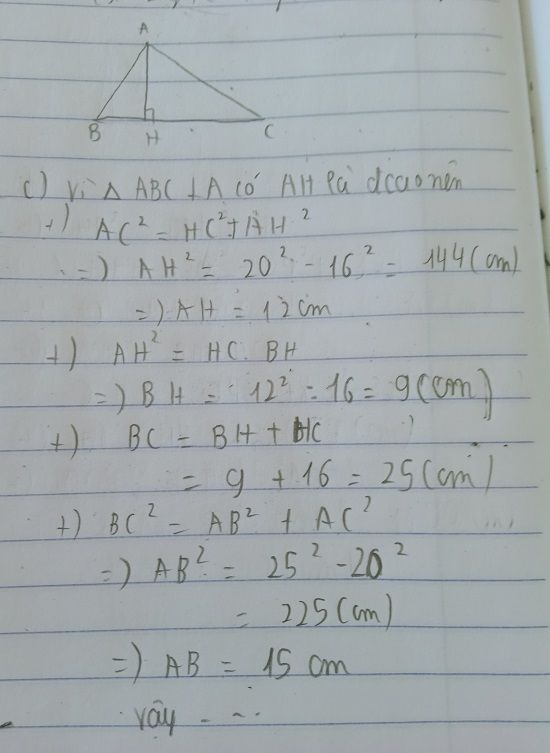Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

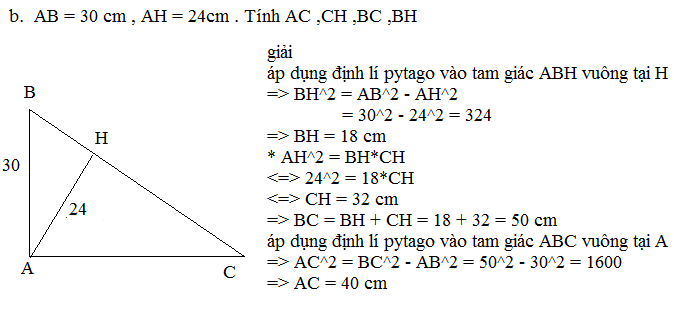
ABCHÁp dụng định lý Py - ta - Go vào tam giác ABC vuông tại A có :
AC2 = BC2 - AB2
AC2 = √52−32=3(AC>0)52−32=3(AC>0)
Ta có : SABC=12AB.ACSABC=12AB.AC
Mà : SABC=12AH.BCSABC=12AH.BC
⇒ 12AB.AC=12AH.BC12AB.AC=12AH.BC
⇔ AH = AB.ACBC=3.45=2,4(cm)
ACBH
a) Áp dụng pi ta go ta có : AB2 = AH2 + BH2 = 162 + 252 = 881
=> AB = √881881
Lại có : BH.HC = AH2
<=> HC.25 = 162
<=> HC.25 = 256
<=> HC = 256 : 25 = 10,24
Ta có : BC = HC + BH = 10,24 + 25 = 35,24
Áp dụng bi ta go : AC2 = AH2 + HC2 = 162 + 10,242 = 360,8576
=> AC = √360,8576

Bài 5:
Ta có: \(AB^2=BH\cdot BC\)
\(\Leftrightarrow BH\left(BH+9\right)=400\)
\(\Leftrightarrow BH^2+25HB-16HB-400=0\)
\(\Leftrightarrow BH=16\left(cm\right)\)
hay BC=25(cm)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\left\{{}\begin{matrix}AC^2=CH\cdot BC\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AC=15\left(cm\right)\\AH=12\left(cm\right)\end{matrix}\right.\)

a)
xét tam giác ABC vuông tại A:
=> tan C= AH/HC=12/15=0.8 (tỉ số lượng giác)
=>C=40 độ
ta có: góc B= 90 độ - góc C (vì C+B=90 vì A=90 )
góc B=90 độ - 40 độ
góc B=50 độ.
xét tam giác ABC vuông tại A có:
Cos B = AH/BH (tỉ số lượng giác)
=> BH=AH/ cos B = 12/cos 50 độ=18.67 cm
b) xét tam giác ABC vuông tại A có:
AB^2 = BH*BC (hệ thức lượng)
AB^2=18.67*25
AB^2=466.7
=>AB=21.6
ta lại có:
AH*BC=AB*AC (hệ thức lượng)
12 * 25= 21.6*AC
=>AC=(12*25)/21.6=13.89 cm
a) Đặt BH=x => CH=BC-BH=25-x
Áp dụng hệ thức giữa cạnh và đường cao vào tam giác ABC vuông tại A, AH vuông góc với BC, ta có:
+) AH2= BH . CH
hay 122= x(25-x)
<=> 144=25x-x2
<=> x2-25x+144=0
<=>(x2-9x)-(16x-144)=0
<=>x(x-9)- 16(x-9)=0
<=>(x-9)(x-16)=0
<=> x-9=0 x=9
<=>
x-16=0 x=16
vì AB<AC nên BH<CH. Mà BC =25=> x=BH=9 cm=> CH= 25-9=16cm
+) AB2=BH. BC=9. 25=225=> AB=15cm
+)AC2=CH. BC= 16.25=400=> AC=20cm
b)Ta có: snB= AC/BC= 0,8=> góc B=53 độ
Xét tam giác ABC có đường trung tuyến AM=> AM=1/2 BC= BM=> tam giác ABM cân tại M => góc B = góc BAM=53 độ
=> AMH hay AMB= 180 độ- ( 53 độ+53 độ)=74 độ
c) Áp dụng định lí Py-ta -go vào tam giác ABH ta có :
BH2= AB2- AH2
hay BH2= 152-122=81=> BH= 9cm
Ta có : BM=1/2 BC=1/2.25=12,5 cm=> HM= BM-BH=12,5-9=3,5cm
=> S tam giác AHM= AH.HM:2=12.3,5:2=21cm2
Có nhiều cách giải, bạn làm theo cách này cx đc

f) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow HB\cdot HC=12^2=144\)(1)
Ta có: BH+CH=BC(H nằm giữa B và C)
nên BH+CH=25
hay BH=25-CH(2)
Thay (2) vào (1), ta được:
\(HC\left(25-HC\right)=144\)
\(\Leftrightarrow HC^2-25HC+144=0\)
\(\Leftrightarrow\left[{}\begin{matrix}HC=16\\HC=9\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}HB=9\\HB=16\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}AB\in\left\{15;20\right\}\\AC\in\left\{20;15\right\}\end{matrix}\right.\)