Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì ∆ ABC đồng dạng với ∆ AMN nên:
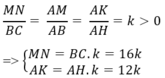
Diện tích hình chữ nhật MNPQ là:
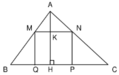
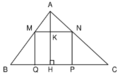
SMNPQ = MN. NP = MN.KH = MN.( AH – AK)
=> SMNPQ = 16k.( 12- 12k)
Theo đề bài diện tích hình chữ nhật đó là 36cm2 nên
16k.( 12- 12k ) = 36
⇔ 16k.12( 1- k) = 36
⇔ 16k(1 – k) = 3 ( chia cả hai vế cho 12)
⇔ 16k – 16k2 = 3
⇔ 16k2- 16k + 3= 0
Ta có: ∆’= (-8)2 – 16.3 = 16> 0
Phương trình trên có 2 nghiệm là:
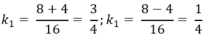
Vậy để diện tích hình chữ nhật MNPQ là 36cm2 thì vị trí điểm M phải thỏa mãn:
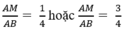

Vì ∆ ABC đồng dạng với ∆ AMN nên:
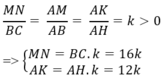
Diện tích hình chữ nhật MNPQ là:
SMNPQ = MN. NP = MN.KH = MN.( AH – AK)
=> SMNPQ = 16k.( 12- 12k)
Theo đề bài diện tích hình chữ nhật đó là 36cm2 nên
16k.( 12- 12k ) = 36
⇔ 16k.12( 1- k) = 36
⇔ 16k(1 – k) = 3 ( chia cả hai vế cho 12)
⇔ 16k – 16k2 = 3
⇔ 16k2- 16k + 3= 0
Ta có: ∆’= (-8)2 – 16.3 = 16> 0
Phương trình trên có 2 nghiệm là:
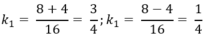
Vậy để diện tích hình chữ nhật MNPQ là 36cm2 thì vị trí điểm M phải thỏa mãn:
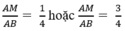

A B C M N Q I H a D
Bạn vẽ hình rồi kí hiệu như trên.
a) \(\dfrac{AB}{AC}=\dfrac{1}{\sqrt{3}}\Rightarrow\dfrac{AB^2}{AC^2}=\dfrac{1}{3}=\dfrac{BH\cdot BC}{CH\cdot BC}=\dfrac{BH}{CH}\)(Cái này áp dụng hệ thức lượng tam giác dạng \(c^2=a\cdot c'\)).
Ta có : \(\left\{{}\begin{matrix}\dfrac{BH}{CH}=\dfrac{1}{3}\\CH-BH=8\end{matrix}\right.\) => Hiệu số phần bằng nhau là 2.
Ta tính được : \(\left\{{}\begin{matrix}CH=\dfrac{8}{2}\cdot3=12\\BH=\dfrac{12}{3}=4\end{matrix}\right.\) => \(BC=BH+CH=16\).
Có \(\dfrac{AB^2}{AC^2}=\dfrac{1}{3}\), mà \(AB^2+AC^2=BC^2=16^2=256\)
Tổng số phần bằng nhau là 4.
\(\Rightarrow\left\{{}\begin{matrix}AB^2=\dfrac{256}{4}=64\\AC^2=\dfrac{256}{4}\cdot3=192\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}AB=8\\AC=8\sqrt{3}\end{matrix}\right.\)
Vậy \(\Delta ABC\) có \(AB=8,AC=8\sqrt{3},BC=16\).
b)\(S_{MNIQ}=MQ\cdot MN=a\cdot MN\) (kí hiệu như hình).
Trong đó : \(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{8\cdot8\sqrt{3}}{16}=4\sqrt{3}\)
+) \(AD=AH-HD=AH-MQ=4\sqrt{3}-a\)
+) \(MN\)//\(BC\Rightarrow\Delta AMN\) đồng dạng với \(\Delta ABC\)
\(\Rightarrow\dfrac{MN}{BC}=\dfrac{AD}{AH}\Rightarrow MN=\dfrac{BC\cdot AD}{AH}\)
\(=\dfrac{16\cdot\left(4\sqrt{3}-a\right)}{4\sqrt{3}}=\dfrac{4\cdot\left(4\sqrt{3}-a\right)}{\sqrt{3}}\)
=> \(S_{MNIQ}=MQ\cdot MN=a\cdot\left(\dfrac{4\cdot\left(4\sqrt{3}-a\right)}{\sqrt{3}}\right)=\dfrac{16\sqrt{3}a-4a^2}{\sqrt{3}}\)
\(=\dfrac{-\left(4a^2-16\sqrt{3}a\right)}{\sqrt{3}}=-\dfrac{\left[\left(2a-4\sqrt{3}\right)^2-48\right]}{\sqrt{3}}\)
\(=\dfrac{48-\left(2a-4\sqrt{3}\right)^2}{\sqrt{3}}=\dfrac{48}{\sqrt{3}}-\dfrac{\left(2a-4\sqrt{3}\right)^2}{\sqrt{3}}\le\dfrac{48}{\sqrt{3}}=16\sqrt{3}\)
Vậy \(S_{MNIQ-max}=16\sqrt{3}\Leftrightarrow a=2\sqrt{3}\).