Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có:
· Trong tam giác ABC thì MP là đường trung bình nên”
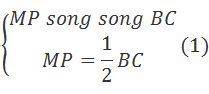
· Trong tam giác OBC ta có MP là đường trung bình nên:
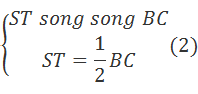
![]()
Suyra:MPTS là hình bình hành. (*)
Ta kiếm góc vuông:
Trong tam giác COA ta có TP là đường trung bình nên TP//AO
=>![]() (3)
(3)
Trong tam giác ABC ta có MP là đường trung bình nên MP//BC
=>![]() (4)
(4)
Từ (3),(4) suy ra: ![]()
Suy ra; ![]()
Từ(*),(**) suy ra MPTS là hình chử nhật.
=>MT=PS và chúng cắt nhau tại trung điểm. (5)
b) chứng minh tương tự câu a ta cũng có:
RPNS là hình chử nhật ,do đó:
RN=PS, và chúng cắt nhau tại trung điểm. (6)
Từ (5),(6), suy ra 3 đoạn RN,MT,SP bằng nhau và cắt nhau tại trung điểm mỗi đường

a) xét tg ABC,có: D là trung điểm AB ; F là trung điểm AC =>DF là đường trung bình tg ABC
=>DF //BC (1)
xét tg ABC , có :D ,E lần lượt là trung điểm AB và BC =>DE là đường trung bình tg ABC =>DE //AC (2)
TỪ (1) và (2) =>CEDF là hbh
TỨ GIÁC ADEF CHỨNG MINH TƯƠNG TỰ =>ADEF LÀ HBH

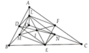
A B C M P O R H Q K N
a) Xét tam giác ABH có: P là trung điểm của AB(gt),Q là trung điểm của AH (gt)
\(\Rightarrow PQ\)là đường trung bình của tam giác ABH
\(\Rightarrow PQ//BH\left(tc\right)\)(1)
Vì \(\hept{\begin{cases}BH\perp AC\\OR\perp AC\end{cases}\Rightarrow BH//}OR\)( từ vuông góc đến song song ) (2)
Từ (1) và (2) \(\Rightarrow PQ//OR\)
Ta có:\(\hept{\begin{cases}OP\perp AB\\CH\perp AB\end{cases}\Rightarrow OP//CH}\)( từ vuông góc đến song song ) (3)
Xét tam giác AHC có Q là trung điểm của AH(gt),R là trung điểm của AC(gt)
\(\Rightarrow QR\)là đường trung bình của tam giác AHC
\(\Rightarrow QR//HC\left(tc\right)\left(4\right)\)
Từ (3) và (4) \(\Rightarrow OP//QR\)
Xét tứ giác PQRO có
\(\hept{\begin{cases}PQ//OR\left(cmt\right)\\OP//QR\left(cmt\right)\end{cases}}\Rightarrow PQRO\)là hình bình hành (dhnb)
b) Để PQRO là hình bình hành \(\Leftrightarrow BH=HC\)
Xét tam giác BHK và tam giác CHK có:
\(\hept{\begin{cases}\widehat{HKB}=\widehat{HKC}=90^0\\HKchung\\BH=HC\left(cmt\right)\end{cases}\Rightarrow\Delta BHK=\Delta CHK\left(ch-cgv\right)}\)
\(\Rightarrow BK=KC\)( 2 cạnh t.ứng )
\(\Rightarrow K\)là trung điểm của BC ( vì K thuộc BC)
Mà M là trung điểm của BC (gt)
\(\Rightarrow K\equiv M\)
Xét tam giác ABC có AK vừa là đường cao vừa là trung tuyến của tam giác ABC
\(\Rightarrow\Delta ABC\)cân tại A.
Vậy để PQRO là hình thoi thì tam giác ABC phải cân tại A.

Gọi I trung điểm LE. Ta có DL//EN//OB và DL = EN = 0.5OB Þ DENL là hình bình hành. Tương tự chứng minh LMEF là hình bình hành. Từ đó suy ra EL,FM, DN đồng quy tại I