Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì MD là trung trực AB trong ∆AMD
=> ∆AMD cân tại A
=> AM = AD
Vì DN là trung trực AC trong ∆ADN
=>∆ADN cân tại A
=> AD = AN
Mà AM = AD
=> AM = AN
=> ∆AMN cân tại A

https://olm.vn/hoi-dap/tim-kiem?q=Cho+tam+gi%C3%A1c+ABC+nh%E1%BB%8Dn,+AD+vu%C3%B4ng+g%C3%B3c+v%E1%BB%9Bi+BC+t%E1%BA%A1i+D.+X%C3%A1c+%C4%91%E1%BB%8Bnh+I,+J+sao+cho+AB+l%C3%A0+trung+tr%E1%BB%A5c+c%E1%BB%A7a+DI;+AC+l%C3%A0+trung+tr%E1%BB%B1c+c%E1%BB%A7a+DJ;+IJ+c%E1%BA%AFt+AB,+AC+l%E1%BA%A7n+l%C6%B0%E1%BB%A3t+%E1%BB%9F+L+v%C3%A0+K.+Ch%E1%BB%A9ng+minh+r%E1%BA%B1ng:++Tam+gi%C3%A1c+AIJ+c%C3%A2n.DA+l%C3%A0+tia+ph%C3%A2n+gi%C3%A1c+c%E1%BB%A7a+g%C3%B3c+LDK.N%E1%BA%BFu+D+l%C3%A0+1+%C4%91i%E1%BB%83m+t%C3%B9y+%C3%BD+tr%C3%AAn+BC.+Ch%E1%BB%A9ng+minh+s%E1%BB%91+%C4%91o+g%C3%B3c+IAJ+kh%C3%B4ng+%C4%91%E1%BB%95i+v%C3%A0+v%E1%BB%8B+tr%C3%AD+D+tr%C3%AAn+BC+%C4%91%E1%BB%83+IJ+nh%E1%BB%8F+nh%E1%BA%A5t.&id=32357
Bạn xem ở link này nhé

a) Ta có: AB là đường trung trực của DM(gt)
⇔A nằm trên đường trung trực của DM
hay AM=AD(tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: AC là đường trung trực của DN(gt)
⇔A nằm trên đường trung trực của DN
hay AD=AN(tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AM=AN
Xét ΔAMN có AM=AN(cmt)
nên ΔAMN cân tại A(định nghĩa tam giác cân)
b) Ta có: AB là đường trung trực của MD(gt)
mà F∈AB(AB\(\cap\)MN={F})
nên FB là đường trung trực của MD
⇔F nằm trên đường trung trực của MD
hay FM=FD(tính chất đường trung trực của một đoạn thẳng)(3)
Ta có: AC là đường trung trực của DN(gt)
mà E∈AC(AC\(\cap\)MN={E})
nên EC là đường trung trực của DN
⇔E nằm trên đường trung trực của DN
hay ED=EN(tính chất đường trung trực của một đoạn thẳng)(4)
Ta có: ME+EN=MN(E nằm giữa M và N)
mà ME=MF+FE(F nằm giữa M và E)
nên MN=MF+FE+EN(5)
Từ (3),(4) và (5) suy ra DE+EF+FD=MN(đpcm)
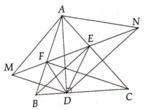


tự kẻ hình nha:333
a) vì AB là trung trực của DM=> MH=HD( đặt H là giao điểm của AB và DM)
xét tam giác MAB và tam giác DAB có
MH=HD(cmt)
AHM=AHD(=90 độ)
AH chung
=> tam giác MAB= tam giác DAB(cgc)
=> AM=AD( hai cạnh tương ứng)
vì AC là trung trực của DN=> NK=DK( đặt K là giao điểm của AC và DN)
xét tam giác AKD và tam giác AKN có
DK=NK(cmt)
AKD=AKN(=90 độ)
AK chung
=> tam giác AKD= tam giác AKN( cgc)
=> AN=AD ( hai cạnh tương ứng)
AM=AD(cmt)
=> AM=AN=> tam giác AMN cân A
b) vì E thuộc đường trung trực AB=> EM=ED
vì F thuộc đường trung trực AC=> FD=FN
ta có MN=ME+EF+FN mà EM=ED, FD=FN
=> MN= ED+EF+FD
c) xét tam giác ADF và tam giác ANF có
FD=FN(cmt)
AD=AN(cmt)
AF chung
=> tam giác ADF= tam giác ANF(ccc)
=> ANF=ADF( hai góc tương ứng)
xét tam giác AME và tam giác ADE có
AM=AD(cmt)
AE chung
EM=ED(cmt)
=> tam giác AME= tam giác ADE(ccc)
=> AME=ADE( hai góc tương ứng)
mà AME=ANF( tam giác AMN cân A)
=> ADE=ADF=> AD là p/g của EDF
d) chưa nghĩ đc :)))))))
CHUẨN R BN ƠI HỌC THÌ NGU MÀ CHƠI NGU THÌ GIỎI