Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: Q và A đối xứng với nhau qua MN
nên MN là đường trung trực của QA
=>MN vuông góc với QA tại trung điểm của QA
Ta có: Q và B đối xứng với nhau qua MP
nên MP là đường trung trực của QB
=>MP vuông góc với QB tại trung điểm của QB
Xét tứ giác MRQS có
\(\widehat{MRQ}=\widehat{MSQ}=\widehat{SMR}=90^0\)
Do đó: MRQS là hình chữ nhật
b: Xét ΔMNP có
Q là trung điểm của NP
QS//MN
Do đó: S là trung điểm của MP
Xét tứ giác MQPB có
S là trung điểm của MP
S là trung điểm của QB
Do đó: MQPB là hình bình hành
mà QM=QP
nên MQPB là hình thoi

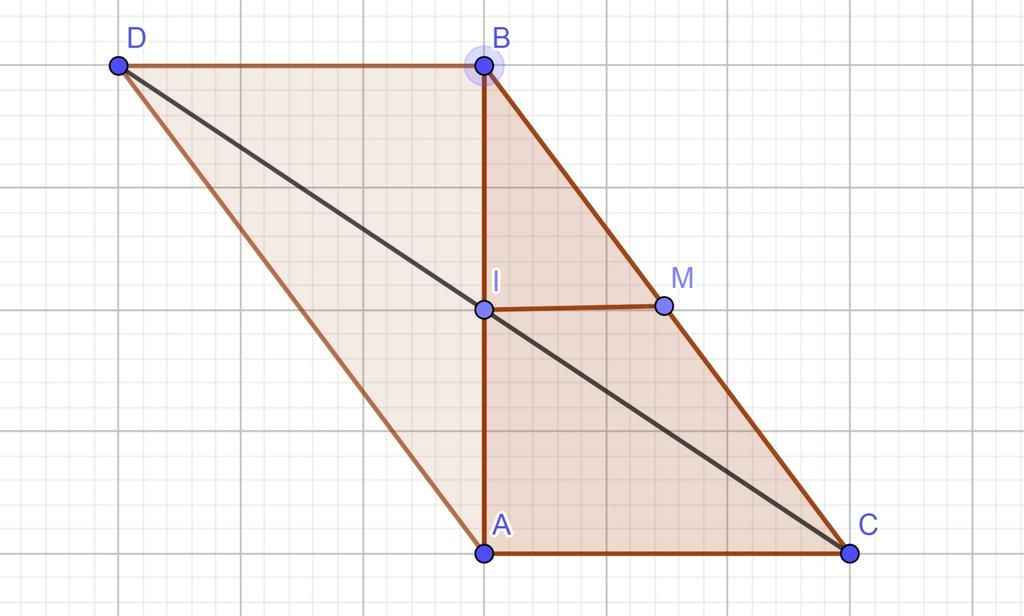
a) Xét tứ giác \(ADBC\) ta có :
\(IB=IA\left(g.t\right)\)
\(IC=IC\) ( \(D\) đối xứng qua \(I\))
Vì tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường
Vậy tứ giác \(ADBC\) là hình bình hành
b) Xét \(\Delta ABC\) ta có :
\(IA=IB\left(g.t\right)\)
\(MB=MC\left(g.t\right)\)
\(\Rightarrow IM\) là đường trung bình \(\Delta ABC\)
Do đó : \(IM\text{/ / }AC\)
Mà \(AB\text{⊥}AC\left(A=90^o\right)\)
Vậy \(IM\text{⊥}AB\)
Áp dụng định lí pytago \(\Delta ABC\) ta có :
\(BC^2=AB^2+AC^2\)
\(\Rightarrow AB=\sqrt{BC^2-AC^2}=\sqrt{13^2-5^2}=12\left(cm\right)\)
\(S_{\Delta ABC}=\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.13.5=30\left(cm^2\right)\)
Phần tính diện tích ∆ABC cậu lộn AB =13cm roii í phải là 1/2 × 12 × 5 = 30 cm nha

a) ta có :
KI vuông góc vs MN (gt),MNvuông góc vs MP (gt), IP' vuông góc vs MP(gt)
suy ra : tứ giác MKIP' là hình chữ nhật(đpcm)
b) ta có : MI = KP (tc hai đường chéo HCN)
suy ra : MF = FI (gt)
KF = P'F = 1/2KP' = 1/2 MF(tc)
vậy 3 đm K,F,P' thẳng hàng
c) ta có :
KI vuông góc vs NM (gt) , mà MN vuông góc vs MP (gt)
suy ra :
KI song song vs MP , có PI = IN (gt)
suy ra : tam giác MNP có KI là ĐBH
suy ra IK bằng 1/2 MP (tc)
có : KI + MP' (hcn) , vậy suy ra : KI = MP' = P'P (tc),vậy MP' = P'P (tc) (1)
có IP' = P'L (tc) (2)
mà IL vuông góc vs MP (gt) (3)
vậy từ (1),(2) và (3) suy ra : tứ giác MIPL là hinh thoi

Sửa đề: DE vuông góc với MP tại F
a) Xét tứ giác MEDF có
\(\widehat{EMF}=90^0\)(\(\widehat{NMP}=90^0\), E∈MN, F∈MP)
\(\widehat{DEM}=90^0\)(DE⊥MN)
\(\widehat{DFM}=90^0\)(DF⊥MP)
Do đó: MEDF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)

hình bạn tự vẽ nhé
a) Xét tứ giác ADBC có AB giao DC tại I là trung điểm của mỗi đường
\(\Rightarrow ADBC\)là hình bình hành (dhnb)
b) Xét tam giác ABC có:
I là trung điểm của AB (gt) , M là trung điểm của BC(gt)
\(\Rightarrow IM\)là đường trung bình tam giác ABC
\(\Rightarrow IM//AC\left(tc\right)\)
Mà \(AB\perp AC\)
\(\Rightarrow IM\perp AB\)( từ vuông góc đến song song )
c) Áp dụng định lý Py-ta-go vào tam giác ABC ta được:
\(AB^2+AC^2=BC^2\)
\(AB^2+5^2=13^2\)
\(AB^2=144\)
\(\Rightarrow AB=12\left(cm\right)\)
\(S_{ABC}=\frac{1}{2}AB.AC=\frac{1}{2}.12.5=30\left(cm^2\right)\)
Vậy ...
a: Xét tứ giác MPNI có
Q là trung điểm chung của MN và PI
Do đó: MPNI là hình bình hành
b: Xét ΔNMP có NQ/NM=NK/NP
nên QK//MP
=>QK vuông góc với MN