K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên

AH
Akai Haruma
Giáo viên
13 tháng 7 2024
Lời giải:
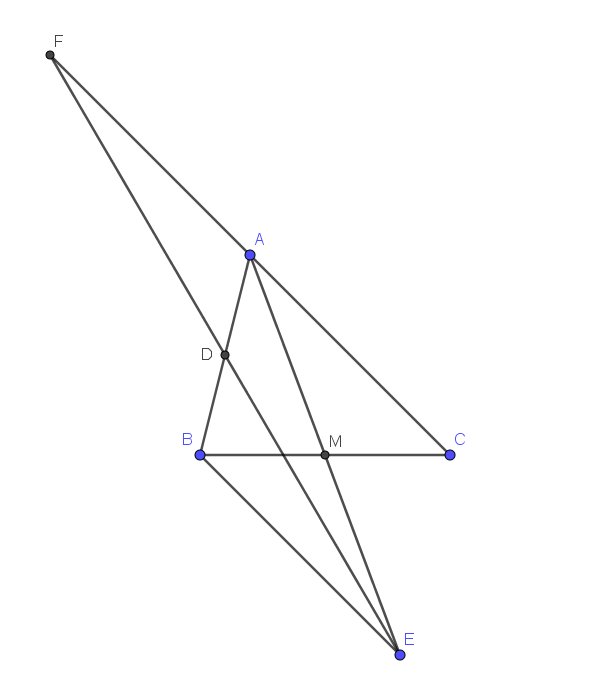
a. Xét tam giác $AMC$ và $EMB$ có:
$AM=ME$
$MB=MC$ (do $M$ là trung điểm $BC$)
$\widehat{AMC}=\widehat{EMB}$ (đối đỉnh)
$\Rightarrow \triangle AMC=\triangle EMB$ (c.g.c)
$\Rightarrow AC=EB$
b. Xét tam giác $AFD$ và $BED$ có:
$FD=ED$
$AD=BD$ (do $D$ là trung điểm $AB$)
$\widehat{ADF}=\widehat{BDE}$ (đối đỉnh)
$\Rightarrow \triangle AFD=\triangle BED$ (c.g.c)
$\Rightarrow AF=BE$
Mà theo phần a thì $AC=BE$ nên $AF=AC$
1) Xét tam giác MNH và tam giác MKH có:
+ MN = MK (gt).
+ MH chung.
+ NH = KH (H là trung điểm NK).
=> Tam giác MNH = Tam giác MKH (c - c - c).
3) Ta có: MD = MN + ND; ME = MK + KE.
Mà ND = KE (gt); MN = MK (gt).
=> MD = ME.
Xét tam giác MNK có: MN = MK (gt).
=> Tam giác MNK cân tại M.
Mà MH là đường trung tuyến (H là trung điểm NK).
=> MH là đường phân giác \(\widehat{M}\) (Tính chất các đường trong tam giác cân).
Xét tam giác HMD và tam giác HME:
+ MD = ME (cmt).
+ \(\widehat{DMH}=\widehat{EMH}\) (MH là đường phân giác \(\widehat{M}\)).
+ MH chung.
=> Tam giác HMD = Tam giác HME (c - g - c).
4) Xét tam giác MDE có: MD = ME (cmtt).
=> Tam giác MDE cân tại M.
Mà MO là đường trung tuyến (O là trung điểm DE).
=> MO là đường phân giác \(\widehat{M}\) (Tính chất các đường trong tam giác cân).
Mà MH là đường phân giác \(\widehat{M}\) (cmt).
=> Ba điểm M, H, O thẳng hàng.
5) Xét tam giác MDE cân tại M có: MO là đường trung tuyến (O là trung điểm DE).
=> MO là đường cao (Tính chất các đường trong tam giác cân).
=> MO \(\perp\) DE. (1)
Xét tam giác MNK cân tại M có: MH là đường trung tuyến (H là trung điểm NK).
=> MH là đường cao (Tính chất các đường trong tam giác cân).
=> MH \(\perp\) NK
Hay MO \(\perp\) NK. (2)
Từ (1) và (2) => NK // DE (Từ vuông góc đến song song).