Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Áp dụng hệ thức lượng trong tam giác vuông vào ΔCAB vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(CH\cdot CB=AC^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔCDB vuông tại C có CA là đường cao ứng với cạnh huyền DB, ta được:
\(AD\cdot AB=CA^2\left(2\right)\)
Từ (1) và (2) suy ra \(CH\cdot CB=AD\cdot AB\)
nho thay co giup em voi em dungf tu giac noi tiep khong dung

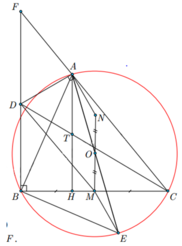
b) CD đi qua trung điểm của đường cao AH của D ABC
· Gọi F là giao của BD và CA.
Ta có BD.BE= BA.BM (cmt)
= > B D B A = B M B E = > Δ B D M ~ Δ B A E ( c − g − c ) = > B M D = B E A
Mà BCF=BEA(cùng chắn AB)
=>BMD=BCF=>MD//CF=>D là trung điểm BF
· Gọi T là giao điểm của CD và AH .
DBCD có TH //BD = > T H B D = C T C D (HQ định lí Te-let) (3)
DFCD có TA //FD = > T A F D = C T C D (HQ định lí Te-let) (4)
Mà BD= FD (D là trung điểm BF ) (5)
· Từ (3), (4) và (5) suy ra TA =TH ÞT là trung điểm AH .

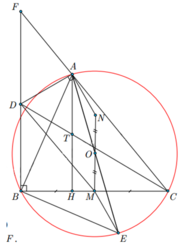
a) Chứng minh BA . BC = 2BD . BE
· Ta có: DBA+ ABC = 900 , EBM +ABC = 900
Þ DBA =EBM (1)
· Ta có: DONA = DOME (c-g-c)
Þ EAN= MEO
Ta lại có: DAB +BAE+ EAN = 900, và BEM +BAE +MEO = 900
Þ DAB= BEM (2)
· Từ (1) và (2) suy ra DBDA đồng dạng DBME (g-g)
= > B D B M = B A B E = > D B . B E = B A . B M = B A . B C 2 = > 2 B D . B E = B A . B C

1: Xét tứ giác BHEK có \(\widehat{BHE}+\widehat{BKE}=180^0\)
nên BHEK là tứ giác nội tiếp
2: Xét ΔBEA vuông tại E có EH là đường cao
nên \(BH\cdot BA=BE^2\left(1\right)\)
Xét ΔBEC vuông tại E có EK là đường cao
nên \(BK\cdot BC=BE^2\left(2\right)\)
Từ (1) và (2) suy ra \(BH\cdot BA=BK\cdot BC\)



a) tam giác AEB vuông tại E có EH là đường cao \(\Rightarrow BH.BA=BE^2\)
tam giác CEB vuông tại E có EK là đường cao \(\Rightarrow BK.BC=BE^2\)
\(\Rightarrow BH.BA=BK.BC\)
b) \(BH.BA=BK.BC\Rightarrow\dfrac{BH}{BC}=\dfrac{BK}{BA}\)
Xét \(\Delta BHK\) và \(\Delta BCA:\) Ta có: \(\left\{{}\begin{matrix}\angle ABCchung\\\dfrac{BH}{BC}=\dfrac{BK}{BA}\end{matrix}\right.\)
\(\Rightarrow\Delta BHK\sim\Delta BCA\left(c-g-c\right)\)
b) \(\Delta BHK\sim\Delta BCA\Rightarrow\angle BHK=\angle BCA\)
Kẻ \(ED\bot CF\)
Vì \(\angle EHF=\angle EDF=\angle HFD=90\Rightarrow EHFD\) là hình chữ nhật
\(\Rightarrow HD\) và EF cắt nhau tại trung điểm I của mỗi đường
Vì \(\Delta EHF\) vuông tại H có I là trung điểm EF
\(\Rightarrow\angle FHI=\angle HFI=\angle AFE\left(1\right)\)
Xét \(\Delta AFC\) và \(\Delta AEB:\) Ta có: \(\left\{{}\begin{matrix}\angle BACchung\\\angle AFC=\angle AEB=90\end{matrix}\right.\)
\(\Rightarrow\Delta AFC\sim\Delta AEB\left(g-g\right)\Rightarrow\dfrac{AF}{AE}=\dfrac{AC}{AB}\Rightarrow\dfrac{AF}{AC}=\dfrac{AE}{AB}\)
Xét \(\Delta AEF\) và \(\Delta ABC:\) Ta có: \(\left\{{}\begin{matrix}\angle BACchung\\\dfrac{AF}{AC}=\dfrac{AE}{AB}\end{matrix}\right.\)
\(\Rightarrow\Delta AEF\sim\Delta ABC\left(c-g-c\right)\Rightarrow\angle AFE=\angle ACB\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\angle FHI=\angle ACB=\angle BHK\Rightarrow\angle BHD=BHK\)
\(\Rightarrow H,D,K\) thẳng hàng \(\Rightarrow H,I,K\) thẳng hàng
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔBEA vuông tại E có EH là đường cao ứng với cạnh huyền AB, ta được:
\(BH\cdot BA=BE^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBEC vuông tại E có EK là đường cao ứng với cạnh huyền AC, ta được:
\(BK\cdot BC=BE^2\)(2)
Từ (1) và (2) suy ra \(BH\cdot BA=BK\cdot BC\)
b) Xét ΔBHK và ΔBCA có
\(\dfrac{BH}{BC}=\dfrac{BK}{BA}\)(cmt)
\(\widehat{HBK}\) chung
Do đó: ΔBHK\(\sim\)ΔBCA(c-g-c)