Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi 3 cạnh của tam giác lần lượt là a , b , c
Theo đề bài ta có :
\(\dfrac{a}{3}=\dfrac{b}{6}=\dfrac{c}{4}=\dfrac{a+b+c}{3+6+4}=\dfrac{36}{13}cm\\ \Rightarrow\left\{{}\begin{matrix}a=3.\dfrac{36}{13}=\dfrac{108}{13}cm\\b=6.\dfrac{36}{13}=\dfrac{216}{13}\\c=4.\dfrac{36}{13}=\dfrac{144}{13}\end{matrix}\right.\)
opps, sai đề r á bn ơi, đề là 3 đường cao chứ ko phải 3 cạnh ah

Gọi chiều cao của tam giác tương ứng a,b,c
Các cạnh của tam giác là x, y, z tương ứng
ta có:\(\dfrac{a}{3}=\dfrac{b}{6}=\dfrac{c}{4}\)
đặt \(\text{}\text{}\dfrac{a}{3}=\dfrac{b}{6}=\dfrac{c}{4}=k\left(k\ne0\right)\Rightarrow a=3k;b=6k;c=4k\\ S_{\Delta}=\dfrac{1}{2}ax=\dfrac{1}{2}by=\dfrac{1}{2}cz\Rightarrow ax=by=cz\)
\(\Rightarrow3k.x=6k.y=4k.z\Rightarrow3x=6y=4z\Rightarrow\dfrac{3x}{12}=\dfrac{6y}{12}=\dfrac{4z}{12}=\dfrac{x}{4}=\dfrac{y}{2}=\dfrac{z}{3}=\dfrac{x+y+z}{4+2+3}=\dfrac{36}{9}=4\\ \Rightarrow\left\{{}\begin{matrix}x=4.4=16\\y=2.4=8\\z=3.4=12\end{matrix}\right.\)

Mình trình bày khác bạn ST CTV nhé :) nhưng cũng đúng
Gọi 3 cạnh của tam giác lần lượt là a , b , c
Theo đề bài ta có :
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{60}{12}=5\)
\(\Rightarrow\)\(a=7.3=21\)
\(b=7.4=28\)
\(c=7.5=35\)
Vậy độ dài 3 cạnh lần lượt dài là 21 cm ; 28 cm ; 35 cm
Gọi 3 cạnh của tam giác là a,b,c
Vì a,b,c tỉ lệ thuận với 3;4;5 nên \(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}\)
Theo tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{3}=\frac{b}{4}=\frac{c}{5}=\frac{a+b+c}{3+4+5}=\frac{60}{12}=5\)
=> a/3 = 5 => a = 15
b/4 = 5 => b = 20
c/5 = 5 => c = 25
Vậy...


lại bắt đầu nè tìm đường cao như bình thường rồi xét đường cao = cạnh => đó là các cạnh bla bla
Gọi chiều cao của tam giác lần lượt là a, b, c
các cạnh của tam giác lần lượt là x, y, z
Ta có: \(\frac{a}{3}=\frac{b}{5}=\frac{c}{6}\)
Đặt \(\frac{a}{3}=\frac{b}{5}=\frac{c}{6}=k\left(k\ne0\right)\)\(\Rightarrow a=3k\), \(b=5k\), \(c=6k\)
\(S_{\Delta}=\frac{1}{2}ax=\frac{1}{2}by=\frac{1}{2}cz\)\(\Rightarrow ax=by=cz\)
\(\Rightarrow3k.x=5k.y=6k.z\)\(\Rightarrow3x=5y=6z\)\(\Rightarrow\frac{3x}{30}=\frac{5y}{30}=\frac{6z}{30}=\frac{x}{10}=\frac{y}{6}=\frac{z}{5}=\frac{x+y+z}{10+6+5}=\frac{42}{21}=2\)
\(\Rightarrow x=2.10=20\), \(y=2.6=12\), \(z=2.5=10\)
Vậy độ dài 3 cạnh của tam giác lần lượt là 20 cm, 12 cm, 10 cm

Gọi x , y , z lần lượt là độ dài các cạnh của tam giác (cm) ( x , y , z > 0 )
Chu vi của tam giác là 36 cm nên x + y + z = 36
Vì các cạnh của tam giác tỉ lệ với các số 3 , 4 , 5 nên x/3 =y/4 = z/5
Theo tính chất dãy tỉ số bằng nhau ta có :
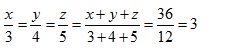
Suy ra : x = 3 . 3 = 9 (TM)
y = 4 . 3 = 12 (TM)
z = 5 . 3 = 15 (TM)
Vậy độ dài các cạnh của tam giác lần lượt là : 9cm , 12cm , 15cm .
mik mới làm xong mà :')
Gọi độ dài ba cạnh của tam giác đó lần lượt là a,b,c và các đường cao tương ứng là x,y,z.
⇒ ax=by=cz(=2S△)
x:y:z=3:6:4 ⇒ \(\dfrac{x}{3}\)=\(\dfrac{y}{6}\)=\(\dfrac{z}{4}\)⇒ \(\dfrac{ax}{3a}=\dfrac{by}{6b}=\dfrac{cz}{4c}\)
Mà ax=by=cz
⇒ 3a=6b=4c ⇒ \(\dfrac{3a}{24}=\dfrac{6b}{24}=\dfrac{4c}{24}\) ⇒ \(\dfrac{a}{8}=\dfrac{b}{4}=\dfrac{c}{6}\)
Có: Chu vi tam giác là 36cm ⇒ a+b+c=36
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{a}{8}=\dfrac{b}{4}=\dfrac{c}{6}\)=\(\dfrac{a+b+c}{8+6+4}=\dfrac{36}{18}=2\)
\(\dfrac{a}{8}=2\) a=2.8 a=16
➩ \(\dfrac{b}{4}=2\) ➩ b=2.4 ➩ b=8
\(\dfrac{c}{6}=2\) c=2.6 c=12
Vậy độ dài 3 cạnh của tam giác lần lượt là 16cm;8cm;12cm.