Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.Ta có: AB=AC ( gt )
=> Tam giác ABC cân tại A
Mà AM là đường trung tuyến => AM cũng là đường cao
=> AM vuông góc với BC
b. Ta có: BH = BC : 2 ( AM là đường trung tuyến )
=> BH = 32 : 2 = 16cm
Áp dụng định lý pitago vào tam giác vuông ABM, có:
\(AB^2=AM^2+BM^2\)
\(\Rightarrow AM=\sqrt{AB^2-BM^2}=\sqrt{34^2-16^2}=\sqrt{900}=30cm\)
c.Xét tam giác vuông BMF và tam giác vuông CME, có:
góc B = góc C ( ABC cân )
BM = CM ( gt )
Vậy tam giác vuông BMF = tam giác vuông CME ( cạnh huyền. góc nhọn)
=> BF = CE ( 2 cạnh tương ứng )
=> AF = AE ( AB = AC; BF = CE )
=> Tam giác AEF cân tại A
=> AM vuông với EF (1)
Mà AM cũng vuông với BC (2)
Từ (1) và (2) suy ra EF//BC
d. ta có: BM = CM ( gt ) (3)
Mà trong tam giác vuông MCE có ME là cạnh huyền
=> \(ME>MC\) (4)
Từ (3) và (4) suy ra \(ME>MB\)

a: Ta có:ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
b: BM=CM=BC/2=16cm
=>AM=30(cm)
c: Xét ΔAFM vuông tại F và ΔAEM vuông tại E có
AM chung
\(\widehat{FAM}=\widehat{EAM}\)
Do đó: ΔAFM=ΔAEM
Suy ra: AF=AE
Xét ΔABC có AF/AB=AE/AC
nên FE//BC

Xét ΔAMB và ΔAMC, ta có:
AB = AC (gt)
BM = CM (vì M là trung điểm BC)
AM cạnh chung
Suy ra: ΔAMB = ΔAMC (c.c.c)
Suy ra: ∠(AMB) = ∠(AMC) (1)
Lại có: ∠(AMB) + ∠(AMC) = 180o (hai góc kề bù) (2)
Từ (1) và (2) suy ra: ∠(AMB) = ∠(AMC) = 90o
Vậy AM ⊥ BC.

Xét tam giác ABM và tam giác ACM có:
AB=AC (GT)
góc B= góc C (GT)
BM=CM (GT)
=> tam giác ABM= tam giác ACM (c.g.c)
=> góc AMB = góc AMC ( 2 góc tương ứng)
Mà góc AMB + góc AMC = 180o (2 góc kề bù)
=>góc AMB= góc AMC = 90o
=> AM vuông góc với BC
Ta có: MB=MC=32/2=16 (cm)
Tam giác AMC vuông tại M
=>theo định lý Py-ta-go:
AM2 = AC2 – MC2 = 900
⇒ AM = 30 (cm)
tam giác ABC cân ở A
tiếp tuyến AM
suy ra : AM vuông góc với BC
mà M là trung điểm của BC (AM là tiếp tuyến) suy ra MB =16cm
áp dụng pytago vào tam giác AMB suy ra AM= 30cm

a)taos tam giác ABC cân tại A và AM là đường trung tuyến
=>AM đồng thời là đương trung trực của tam giác ABC tại A
=>AM \(\perp\)vói BC
b)ta có BM=MC mà BC =32 cm
=>BM=MC=32:2=16cm
áp dụng định lí Py ta go cho tam giác vuông AMC ta đc
\(34^2=16^2+AM^2\)
\(=>1156=256+AM^2\)
=>\(1156-256=AM^2\)
Vậy \(AM^2\)= 900=>AM=30CM
a. Xét ΔAMB và ΔAMC, ta có:
AM = AC (gt)
BM = CM (gt)
AM cạnh chung
Suy ra: ΔAMB = ΔAMC (c.c.c)
Suy ra: ∠(AMB) = ∠(AMC) (1)
Lại có: ∠(AMB) + ∠(AMC) = 180o (hai góc kề bù) (2)
Từ (1) và (2) suy ra: ∠(AMB) = ∠(AMC) = 90o
Vậy AM ⊥ BC.
b. Tam giác AMB có ∠(AMB) = 90o
Áp dụng định lí Pi-ta-go vào tam giác vuông AMB, ta có:
AB2 = AM2 + BM2 ⇒ AM2 = AB2 - BM2 = 342 - 162
= 1156 - 256 = 900
Suy ra: AM = 30 (cm).

Ta có:AM là trung tuyến tam giác ABC
=> MB=MC=BC/2=32/2=16 (cm)
=> AM=MB=MC=16 cm ( gt)
Vì đường trung tuyến đi qua trung điểm của
đoạn thẳng BC
Suy ra: BM=CM=32:2=16cm
Xét tam giác ABM và AMC
AB=AC(gt)
AM là cạnh chung
MB=MC(gt)
\(\Rightarrow\)tam giác ABM=tam giác AMC(c.c.c)
Do đó góc AMB=góc AMC(1)
Mà góc AMB+gócAMC=180(kề bù)(2)
Từ 1 và 2 suy ra góc AMB= góc AMC=90 độ
Xét tam giác ABM vuông tại M
Áp dụng định lý Pi-Ta-Go ta có
AM2+BM2=AB2
AM2+162=342
AM=342-162=900
AM=30
vậy AM=30 cm

Do M là trung điểm của BC nên BM = CM = BC/2 cm
Tam giác AMB có ∠(AMB) = 90o
Áp dụng định lí Pi-ta-go vào tam giác vuông AMB, ta có:
AB2 = AM2 + BM2 ⇒ AM2 = AB2 - BM2 = 342 - 162
= 1156 - 256 = 900
Suy ra: AM = 30 (cm).

câu 2 :
a) có phải là chứng minh AM ⊥ BC không
xét ΔAMB và ΔAMC, ta có :
AB = AC (2 cạnh bên của ΔABC cân tại A)
MB = MC (AM là đường trung tuyến của cạnh BC)
AM là cạnh chung
=> ΔAMB = ΔAMC (c.c.c)
=> \(\widehat{AMB}=\widehat{AMC}\) (2 cạnh tương ứng)
mà \(\widehat{AMB}+\widehat{AMC}=180^O\) (kề bù)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}=\dfrac{180^O}{2}=90^O\)
=> AM ⊥ BC
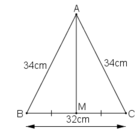
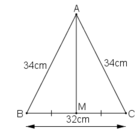

a) Tam giác ABC cân tại A
Trung tuyến AM
=> AM lập tức là đường cao
=> AM vuông góc với BC ( đpcm )
b) Trung tuyến AM => M là trung điểm của BC
=> BM = CM = BC/2 = 32/2 = 16cm
AM vuông góc với BC
=> Tam giác AMB và tam giác AMC vuông
Áp dụng định lí Pytago cho tam giác vuông AMB ta được :
AB2 = AM2 + BM2
<=> 342 = AM2 + 162
<=> \(AM=\sqrt{34^2-16^2}=30\left(cm\right)\)