Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì tam giác ADE có góc D=góc E nên ADE cân tại A.Gọi giao điểm của DM và EN là O.
Xét tam giác DON và tam giá EOM ta có:
góc ODN=góc OEM
DO=EO
góc DON=góc EOM(2 góc đối đỉnh)
=>tam giác DON=tam giác EOM(g.c.g)
=>DN=EM(2 cạnh tương ứng)

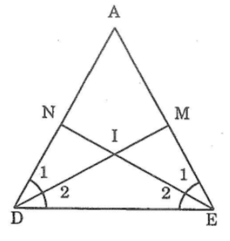
Tam giác ADE có: ∠D = ∠E (giả thiết) (1)
∠(D1) = ∠(D2) = (1/2)∠D (vì DM là tia phân giác của góc ADE) (2)
∠(E1) = ∠(E2) = (1/2)∠E (vì EN là tia phân giác của góc AED) (3)
Từ (1); (2) và (3) suy ra: ∠(D1 ) = ∠(D2) = ∠(E1) = ∠(E2 )
+) Xét ΔDNE và ΔEMD, ta có:
∠(NDE) = ∠(MED) (giả thiết)
DE cạnh chung
∠(D2) = ∠(E2 ) (chứng minh trên)
Suy ra: ΔDNE = ΔEMD (g.c.g)
Vậy DN = EM (hai cạnh tương ứng)

A D E M N 1 2 1 2
Có: Góc D = góc E => tam giác ADE cân tại A (1)
góc D = góc E mà D1 = D2
E1 = E2
=> D1 = E1 (2)
Xét 2 tam giác: ADM và AEN, có:
AD = AE (tam giác ADE cân tại A), (1)
 là góc chung
D1 = D1 (2)
=> tam giác ADM = tam giác AEN (g.c.g)
=> DM = EN (2 cạnh tương ứng)

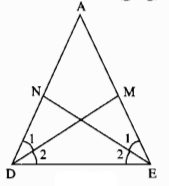
Tam giác ADE có: \(\widehat{\text{D}}=\widehat{E}\)(gt)
\(\widehat{\text{D1}}=\widehat{D2}=\dfrac{1}{2}\widehat{D}\)(Vì DM là tia phân giác)
\(\widehat{\text{E1}}=\widehat{E2}=\dfrac{1}{2}\widehat{E}\)(Vì EN là tia phân giác)
Suy ra:\(\widehat{\text{D1}}=\widehat{D2}=\)\(\widehat{\text{E1}}=\widehat{E2}\)
Xét ∆DNE = ∆EMD, ta có:
\(\widehat{NDE}\widehat{=MED}\)((gt)
DE cạnh chung
\(\widehat{\text{D1}}=\widehat{E2}=\)(chứng minh trên)
Suy ra: ∆DNE = ∆EMD (g.c.g)
Vậy DE = EM (2 cạnh tương ứng).

Vì \(\Delta ADE\) có \(\widehat{D}=\widehat{E}\) nên \(\Delta ADE\) cân tại \(A\).
Xét \(\Delta DON\) và \(\Delta EOM\), ta có:
\(\widehat{ODN}=\widehat{OEM}\)
\(DO=EO\)
\(\widehat{DON}=\widehat{EOM}\)(2 góc đối đỉnh)
\(\Rightarrow\Delta DON=\Delta EOM\left(g.c.g\right)\)
\(\Rightarrow DN=EM\) (2 cạnh tương ứng)

1. A B C D F 1 2 2 1 1 2. A B H D M C
1.Lấy F trên AC sao cho AB = AF mà AB < AC => AF < AC => F nằm giữa A,C
\(\Delta ADB,\Delta ADF\)có AD chung ; AB = AF ;\(\widehat{A_1}=\widehat{A_2}\)(AD là phân giác góc BAC)\(\Rightarrow\Delta ADB=\Delta ADF\left(c.g.c\right)\)
\(\Rightarrow\widehat{D_1}=\widehat{D_2}\); DB = DF mà\(\widehat{F_1}>\widehat{D_1};\widehat{D_2}>\widehat{C}\)(\(\widehat{F_1};\widehat{D_1}\)lần lượt là góc ngoài\(\Delta ADF,\Delta ADC\))nên\(\widehat{F_1}>\widehat{C}\)
\(\Delta DFC\)có\(\widehat{F_1}>\widehat{C}\)nên DC > DF = DB.Vậy BD < CD
2.Theo chứng minh câu 1,ta được BD < CD
\(\Rightarrow BC=BD+CD=2BD+CD-BD\Rightarrow2BD< BC\Rightarrow BD< \frac{BC}{2}\left(=BM\right)\)
=> D nằm giữa B,M => AD nằm giữa AB,AM (1)
\(\Delta ABC\)có AB < AC nên\(\widehat{B}>\widehat{C}\)mà\(\widehat{BAH}=90^0-\widehat{B};\widehat{CAH}=90^0-\widehat{C}\)(vì\(\Delta AHB,\Delta AHC\)vuông tại H)
\(\Rightarrow\widehat{BAH}< \widehat{CAH}\)
\(\Rightarrow\widehat{BAC}=\widehat{BAH}+\widehat{CAH}=2\widehat{BAH}+\widehat{CAH}-\widehat{BAH}\Rightarrow2\widehat{BAH}< \widehat{BAC}\Rightarrow\widehat{BAH}< \frac{\widehat{BAC}}{2}\left(=\widehat{BAD}\right)\)
=> AH nằm giữa AB,AD (2).Từ (1) và (2),ta có đpcm