Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, HS tự chứng minh
b, M chính giữa A B ⏜
=> NE là phân giác B N A ^
=> B N A N = E B E A (tính chất đường phân giác) => BN.AE = NA.BE
c, HS tự chứng minh
d, Chứng minh ∆ABN:∆DBN => ĐPCM

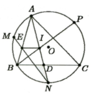
a) ta có :
P là điểm chính giữa cung AC
=> cung AP = cung PC
N là điểm chính giữa cung BC
=> cung NB = NC
Mà : góc IBN = 1/2 cung PN = 1/2 (cung PC + cung CN )
góc BIN = 1/2 ( cung BN + AP )
mà cung PC = cung AP
cung BN = cung CN
=> IBN = BIN
=> tam giác IBN là tam giác cân
b) ta có : N là điểm chính giữa của cung BC
=>MN là tia phân giác của góc BAC
=> EB/AE=BN/AN
=> đpcm
c) ta có : BNI cân
NM là tia phân giác
=> NM cũng là tia trung trực
=> EBN = EIN
MÀ IBN = BIN ( tam giác cân )
=> EBI=EIB (1)
=> tam giác EBI cân
mà P là điểm chính giữa cung AC
=> BP là đường phân giác của góc EBN
=> EBP = IBN hay EBI=IBN (2)
từ (1) và (2) => IBN=EIB
mà 2 góc ở vị trí slt => EI//BC
d) Xét tam giác BAN và tam giác BDN
có N chung
góc BAN = BDN ( cùng chắn cung BN )
=> tam giác BAN đồng dạng tam giác BDN
=> đpcm
a, CM BIN=IBN = 1/2 sđ PN => tam giác BIN cân tại N
b, CM đc MN vuông góc với BP mà tam giác BIN cân tại N => MN là đường trung trực của BI , E thuộc MN => BE=BI và EN là tia pg của BEI
CM tam giác AEN ~ tam giác IEN ( g-g) =>AE.IN = EI.AN => AE.BN = EB.AN
c, CM đc EBP = PBC mà EBI =EIB nên EIB = IBD mà 2 góc này ở vị trí slt=> EI //BC
d, CM tam giác ABN~ tam giác BDN ( g-g) => AN/BN = AB /BD \dfrac{AN}{BN}=\dfrac{AB}{BD}

Ta có: ΔABC đều, D ∈ AB, DE⊥AB, E ∈ BC
=> ΔBDE có các góc với số đo lần lượt là: 300
; 600
; 900
=> BD=1/2BE
Mà BD=1/3BA => BD=1/2AD => AD=BE => AB-AD=BC-BE (Do AB=BC)
=> BD=CE.
Xét ΔBDE và ΔCEF: ^BDE=^CEF=900
; BD=CE; ^DBE=^ECF=600
=> ΔBDE=ΔCEF (g.c.g) => BE=CF => BC-BE=AC-CF => CE=AF=BD
Xét ΔBDE và ΔAFD: BE=AD; ^DBE=^FAD=600
; BD=AF => ΔBDE=ΔAFD (c.g.c)
=> ^BDE=^AFD=900
=>DF⊥AC (đpcm).
b) Ta có: ΔBDE=ΔCEF=ΔAFD (cmt) => DE=EF=FD (các cạnh tương ứng)
=> Δ DEF đều (đpcm).
c) Δ DEF đều (cmt) => DE=EF=FD. Mà DF=FM=EN=DP => DF+FN=FE+EN=DE+DP <=> DM=FN=EP
Lại có: ^DEF=^DFE=^EDF=600=> ^PDM=^MFN=^NEP=1200
(Kề bù)
=> ΔPDM=ΔMFN=ΔNEP (c.g.c) => PM=MN=NP => ΔMNP là tam giác đều.
d) Gọi AH; BI; CK lần lượt là các trung tuyến của ΔABC, chúng cắt nhau tại O.
=> O là trọng tâm ΔABC (1)
Do ΔABC đều nên AH;BI;BK cũng là phân giác trong của tam giác => ^OAF=^OBD=^OCE=300
Đồng thời là tâm đường tròn ngoại tiếp tam giác => OA=OB=OC
Xét 3 tam giác: ΔOAF; ΔOBD và ΔOCE:
AF=BD=CE
^OAF=^OBD=^OCE => ΔOAF=ΔOBD=ΔOCE (c.g.c)
OA=OB=OC
=> OF=OD=OE => O là giao 3 đường trung trực Δ DEF hay O là trọng tâm Δ DEF (2)
(Do tam giác DEF đề )
/
(Do tam giác DEF đều)
Dễ dàng c/m ^OFD=^OEF=^ODE=300
=> ^OFM=^OEN=^ODP (Kề bù)
Xét 3 tam giác: ΔODP; ΔOEN; ΔOFM:
OD=OE=OF
^ODP=^OEN=^OFM => ΔODP=ΔOEN=ΔOFM (c.g.c)
OD=OE=OF (Tự c/m)
=> OP=ON=OM (Các cạnh tương ứng) => O là giao 3 đường trung trực của ΔMNP
hay O là trọng tâm ΔMNP (3)
Từ (1); (2) và (3) => ΔABC; Δ DEF và ΔMNP có chung trọng tâm (đpcm).
A B N E P Q C D
gọi AD là tia phân giác \(\widehat{BAN}\)
\(\Delta BAN\)cân tại A có AD là tia phân giác nên cũng là đường trung tuyến \(\Rightarrow BD=DN\)
Mặt khác : BP = PC
Xét \(\Delta BNC\)có BD = DN ; BP = PC nên DP là đường trung bình
\(\Rightarrow DP//NC\)và \(DP=\frac{1}{2}NC\)
Mà AN = EC hay AE + EN = EN + NC \(\Rightarrow AE=NC\)
\(\Rightarrow DP=\frac{1}{2}AE\)hay \(DP=AQ\)( do AQ = QE ) ( 1 )
Ta có : \(DP//NC\)hay \(DP//AQ\) ( 2 )
Từ ( 1 ) và ( 2 ) suy ra AQPD là hình bình hành \(\Rightarrow PQ//AD\)