Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D E K M
Theo tính chất phân giác: \(\dfrac{BD}{AB}=\dfrac{CD}{AC}\Rightarrow\dfrac{BD}{CD}=\dfrac{AB}{AC}\)
\(\Rightarrow\dfrac{BD}{BD+CD}=\dfrac{AB}{AB+AC}=\dfrac{16}{16+24}=\dfrac{2}{5}\Rightarrow\dfrac{BD}{BC}=\dfrac{2}{5}\)
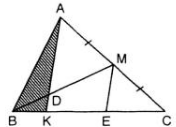
Kẻ DM//BK với \(M\in AC\)
Trong tam giác ADM, áp dụng talet: \(\dfrac{AK}{KM}=\dfrac{AE}{ED}=\dfrac{3}{2}\)
Trong tam giác CBK, áp dụng talet: \(\dfrac{KM}{KC}=\dfrac{BD}{BC}=\dfrac{2}{5}\)
\(\Rightarrow\dfrac{AK}{KM}.\dfrac{KM}{KC}=\dfrac{3}{2}.\dfrac{2}{5}=\dfrac{3}{5}\Rightarrow\dfrac{AK}{KC}=\dfrac{3}{5}\Rightarrow AK=\dfrac{3}{5}KC\)
Mà \(AK+KC=AC=24\Rightarrow\dfrac{3}{5}KC+KC=24\)
\(\Rightarrow\dfrac{8}{5}KC=24\Rightarrow KC=15\)
\(\Rightarrow AK=\dfrac{3}{5}KC=9\)

Bài 1:
Gọi G là trung điểm của BK
Xét ΔBKC có
M là trung điểm của BC
G là trung điểm của BK
Do đó; MG là đường trung bình
=>MG//KC
hay KI//GM
Xét ΔAGM có
I là trung điểm của AM
IK//GM
Do đó; K là trung điểm của AG
=>AK=KG=GB
=>AK=1/3AB