Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định lí Py-ta-go vào tgABH ta được:
\(AB^2=AH^2+BH^2\)
Mà AH=12;BH=5
\(\Rightarrow AB^2=12^2+5^2\)
\(\Rightarrow AB^2=144+25=169\)
\(\Rightarrow AB=13\left(cm\right)\left(doAB>0\right)\)
Áp dụng định lí Py-ta-go vào tg ACH ta được:

Tam giác AHC vuông tại H nên :
AC2 = AH2 + HC2
202 = 122 + HC2
=> HC2 = 202 - 122
HC2 = 400 - 144 = 256 = 162
=> HC = 16 cm
Ta có : BC = HC + HB = 16 + 5 = 21 cm
Tam giác ABH vuông tại H nên :
AB2 = AH2 + HB2
AB2 = 122 + 52
AB2 = 144 + 25 = 169 = 132
=> AB = 13 cm
Vậy chu vi tam giác ABC là :
AB + AC + BC = 13 + 20 + 21 = 54 (cm)

A B C H 16 12 5
Áp dụng định lí Pytago vào tam giác vuông AHC ta có :
\(AC^2=AH^2+HC^2\)
\(AC^2=12^2+16^2\)
\(AC^2=144+256\)
\(AC^2=400\)
\(AC=\sqrt{400}\)
\(AC=20\left(cm\right)\)
Áp dụng định lí Pytago vào tam giác vuông AHB ta có :
\(AB^2=AH^2+BH^2\)
\(AB^2=12^2+5^2\)
\(AB^2=144+25\)
\(AB^2=169\)
\(AB=\sqrt{169}\)
\(AB=13\left(cm\right)\)
Chu vi tam giác ABC là:
\(AB+AC+BC=AB+AC+\left(BH+HC\right)=13+20+\left(5+16\right)=13+20+21=54\left(cm\right)\)
theo định lí pitago trong
tam giác vuông ABH ta có \(AB^2=BH^2+AH^2=5^2+12^2=169\)
=> AB=13
tam giác vuông AHC có : \(AC^2=AH^2+HC^2=12^2+16^2=400\)
=> AC=20
=> chu vi tam giác ABC là AB+BC+AC=13+5+16+20=54
A B H C

A B H C
Xét \(\Delta\)AHC vuông tại H:
=> AC2 = HA2 + HC2
HC2 = AC2 - HA2
HC2 = 202 - 122 = 256
HC = \(\sqrt{256}\) = 16 (cm)
BC = BH + HC
BC = 5 + 16 = 21 (cm)
Xét \(\Delta\)AHB vuông tại H
=> AB2 = HA2 + HB2
AB2 = 122 + 52
AB2 = 144 + 25 = 169
AB = \(\sqrt{169}\) = 13 (cm)
Chu vi của \(\Delta\)ABC là:
AC + CB + BA = 20 + 21 + 13
= 54 (cm)
Vậy chu vi của \(\Delta\)ABC là 54 cm.

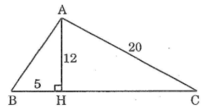
∆AHB có ∠(AHB) =90°
Theo định lý pitago, ta có:
AB2=AH2+HB2
= 122+52=169
Vậy AB = 13 cm
∆AHC có ∠(AHC) =90o
Theo định lý pitago, ta có:
AC2=AH2+HC2
HC2=AC2-AH2=202-122=400-144=256
Vậy HC = 16cm
Ta có: BC = BH + HC = 5 +16 = 21cm
Chu vi tam giác ABC là: AB + AC + BC = 13 + 20 + 21 = 54cm

A H C B 5 12 20 Áp dụng định lý Pytago cho 2 tam giác ABH và ACH ta có AB=13 và HC=16
suy ra chu vi ABC= AC+AB+BH+CH=20+13+5+16=54
Theo mình nghĩ là đúng!:)