Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng Ta lét trong tam giác ABC (EF//BC),ta có
\(\frac{AE}{AB}=\frac{AF}{AC}=\frac{EF}{BC}\Leftrightarrow\frac{3}{3+6}=\frac{1}{3}=\frac{AF}{AF+5}=\frac{6}{BC}\)
NÊN \(\frac{AF}{AF+5}=\frac{1}{3}\Leftrightarrow3AF=AF+5\Leftrightarrow AF=\frac{5}{2}\)
\(\Rightarrow AC=AF+FC=2,5+5=7,5\)
\(\frac{6}{BC}=\frac{1}{3}\Leftrightarrow BC=18\)

Xét ΔABC có FE//BC
nên \(\dfrac{AE}{EB}=\dfrac{AF}{FC}\)
=>\(\dfrac{3}{FC}=\dfrac{6}{10}=\dfrac{3}{5}\)
=>FC=5(cm)

a) Áp dụng định lý Ta-let vào \(\Delta\)ABC, ta có:
\(\frac{AE}{BE}=\frac{AF}{FC}\)
\(\rightarrow\frac{6}{3}=\frac{x}{4}\)
\(\rightarrow x=8\)
Gọi AD là a, ta có:
\(\frac{AF}{FC}=\frac{AD}{DC}\)
\(\rightarrow\frac{6}{3}=\frac{a}{6}\)
\(\rightarrow a=12\)
Vậy:
\(\frac{AE}{BE}=\frac{AD}{BD}\)
\(\rightarrow\frac{6}{3}=\frac{12}{y}\)
\(\rightarrow y=6\)
Áp dụng hệ quả TaLet vào \(\Delta\)ABC, ta có:
\(\frac{EF}{BC}=\frac{AE}{BE}\)
\(\rightarrow\frac{z}{12}=\frac{6}{3}\)
\(\rightarrow z=24\)

gọi cạnh AF là x,BC là y
ta có AB=AE+EB=3+6=9cm;
theo định lý Ta Lét đảo ,ta có :
AE/EB=AF/FC hay 3/6 = x/5
<=>3.5=6.x<=>15=6.x<=> x=2,5
=> AC =AF+FC=2,5+5=7,5cm
mặc khác ta có:
AE/AB=EF/BC hay 3/6=8/y
<=>3.y=6.8<=>3.y=48<=>y=16
=>BC=16cm

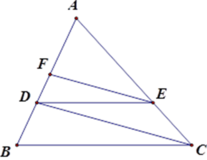
Áp dụng định lý Ta-lét:
Với EF // CD ta có A F A D = A E A C
Với DE // BC ta có A E A C = A D A B
Suy ra A F A D = A D A B , tức là A F 6 = 6 9
Vậy AF = 6.6 9 = 4 cm
Đáp án: C

a: Xét ΔAEF có
D là trung điểm của AE
DG//EF
Do đó: G là trung điểm của AF
Suy ra: AG=GF(1)
Xét hình thang BDGC có
E là trung điểm của DB
EF//DG//BC
Do đó: F là trung điểm của GC
Suy ra: GF=FC(2)
Từ (1) và (2) suy ra AG=GF=FC
b: Xét ΔAFE có
D là trung điểm của AE
G là trung điểm của AF
Do đó:DG là đường trung bình của ΔAFE
Suy ra: \(DG=\dfrac{EF}{2}\)
hay EF=10cm
Hình thang DGCB có
E là trung điểm của DB
F là trung điểm của GC
Do đó: EF là đường trung bình của hình thang DGCB
Suy ra: \(EF=\dfrac{DG+BC}{2}\)
\(\Leftrightarrow10=\dfrac{5+BC}{2}\)
hay BC=15(cm)
Ta có : EF // BC ⇒ ΔAEF đồng dạng ΔABC
⇒ \(\dfrac{AE}{AB}=\dfrac{EF}{BC}\) mà AB = AE + EB = 3 + 5 = 8 cm
⇒ \(EF=\dfrac{AE.BC}{AB}=\dfrac{3.6}{8}=2,25cm\)
Vậy EF = 2,25 cm
cảm ơn