Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

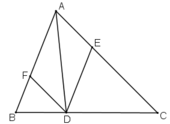
a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
d) Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).

a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
d) Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).
A E F C D B
a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt)
(theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ∆ABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật vừa là hình thoi).

A B C F D E
a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE ( gt ) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu \(\Delta ABC\) vuông tại A thì AEDF là hình chữ nhật ( vì là hình bình hành có một góc vuông )
d) Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông ( vì vừa là hình chữ nhật, vừa là hình thoi )

a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).

a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt)
(theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ∆ABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật vừa là hình thoi).

a) Tứ giác AEDF là hình bình hành.
Vì có DE // AF, DF // AE (gt) (theo định nghĩa)
b) Hình bình hành AEDF là hình thoi khi AD là tia phân giác của góc A. Vậy nếu D là giao điểm của tia phân giác góc A với cạnh BC thì AEDF là hình thoi.
c) Nếu ΔABC vuông tại A thì AEDF là hình chữ nhật (vì là hình bình hành có một góc vuông).
Nếu ABC vuông tại A và D là giao điểm của tia phân giác của góc A với cạnh BC thì AEDF là hình vuông (vì vừa là hình chữ nhật, vừa là hình thoi).

a) Xét tứ giác AEDF có
DE//AF(DE//AB, F\(\in\)AB)
DF//AE(DF//AC, E\(\in\)AC)
Do đó: AEDF là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Hình bình hành AEDF có \(\widehat{EAF}=90^0\)(\(\widehat{BAC}=90^0\), F\(\in\)AB, E\(\in\)AC)
nên AEDF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
b) Hình chữ nhật AEDF trở thành hình vuông khi AD là tia phân giác của \(\widehat{FAE}\)
hay AD là tia phân giác của \(\widehat{BAC}\))
Vậy: Khi D là chân đường phân giác kẻ từ A xuống cạnh BC thì tứ giác AEDF trở thành hình vuông