Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

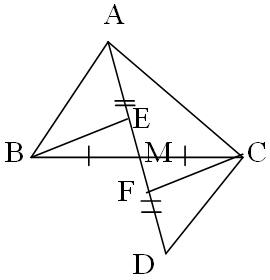
a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMDC
=>\(\widehat{MAB}=\widehat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
b: Xét ΔEMB vuông tại E và ΔFMC vuông tại F có
MB=MC
\(\widehat{EMB}=\widehat{FMC}\)(hai góc đối đỉnh)
Do đó: ΔEMB=ΔFMC
=>EM=FM
=>M là trung điểm của EF

A B C D E F M
a) Xét ΔABM và ΔDCM có:
BM=CM(gt)
\(\widehat{AMB}=\widehat{DMC}\left(đđ\right)\)
AM=DM(gt)
=>ΔABM=ΔDCM(c.g.c)
b) Vì ΔABM=ΔDCM(cmt)
=>\(\widehat{ABM}=\widehat{DCM}\). Mà hai góc này pử vị trí sole trong
=>AB//DC
c)Xét ΔEBM và ΔFCM có:
\(\widehat{BEM}=\widehat{CFM}=90^o\)
BM=MC(gt)
\(\widehat{BME}=\widehat{CMF}\left(đđ\right)\)
=>ΔEBM=ΔFCM( cạnh huyền-góc nhọn)
=>ME=MF
=>M là trung điểm của EF
a) Xét ΔABM và ΔDCM, có:
MB = MC (gt)
∠AMB = ∠DCM (đối đỉnh)
MA = MD (gt)
Vậy ΔABM = ΔDCM (c-g-c)
b) Từ ΔABM = ΔDCM (chứng minh câu a)
Suy ra: ∠ABM = ∠ DCM (hai góc tương ứng)
Mà hai góc ∠ABM và ∠DCM ở vị trí so le trong
Vậy AB // DC
c) Xét ΔBEM và ΔCFM (∠E = ∠F = 90º)
Có: MB = MC (gt)
∠AMB = ∠DMC (đối đỉnh)
Do đó: ΔBEM = ΔCFM (cạnh huyền-góc nhọn)
Suy ra: ME = MF (hai cạnh tương ứng)
Vậy M là trung điểm của EF

A B C E M F D
a ) Xét \(\Delta ABM\)và \(\Delta DCB\) có :
BM = CM (gt)
\(\widehat{AMB}=\widehat{DMC}\left(đđ\right)\)
AM = DM (gt)
\(\Rightarrow\Delta ABM=\Delta DCM\left(c.g.c\right)\)
Vì : \(\Delta ABM=\Delta DCM\left(cmt\right)\)
\(\Rightarrow\widehat{ABM}=\widehat{DCM}\) . Mà 2 góc này ở vị trí so le trong
\(\Rightarrow\) AB // DC
c ) Xét \(\Delta EBM\) và \(\Delta FCM\) có :
\(\widehat{BEM}=\widehat{CFM}=90^o\)
BM = MC (gt)
\(\widehat{BME}=\widehat{CMF}\left(đđ\right)\)
\(\Rightarrow\Delta EBM=\Delta FCM\)(cạnh huyền - góc nhọn )
\(\Rightarrow ME=MF\)
\(\Rightarrow M\) là trung điểm của EF ( đpcm)
Chúc bạn học tốt !!!

a: Xét ΔABM và ΔDCM có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔABM=ΔDCM
b: ta có: ΔABM=ΔDCM
=>\(\widehat{MAB}=\widehat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//DC
c: Xét ΔMEB vuông tại E và ΔMFC vuông tại F có
MB=MC
\(\widehat{EMB}=\widehat{FMC}\)(hai góc đối đỉnh)
Do đó: ΔMEB=ΔMFC
=>ME=MF
mà M nằm giữa E và F
nên M là trung điểm của EF

a) xét tg ABM & tg DCM có
MB=MC (vì M là trung điểm BC)
AMB^ =DMC^(2 GÓC ĐỐI ĐỈNH)
MA =MD (GT)
=) tg ABM=tg DCM(c.g.c)
vậy.......
b) Vì tg ABC =TG DCM nên ABM^ =DCM^ (2 góc tương ứng)
Mà ABM^ & DCM^ ở vị trí so le trong nên AB//DC
vậy.....
c) bó tay
Bạn o0o đồ khùng o0o làm đúng rồi
Bạn  Ngọc My Lovely làm theo cách bạn ấy nha
Ngọc My Lovely làm theo cách bạn ấy nha
Ai thấy mình nói đúng thì nha

a: Xét ΔABM và ΔDCM có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔABM=ΔDCM
b: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó:ABDC là hình bình hành
Suy ra: AB//CD
c: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM la đường cao

a: Xét ΔABM và ΔDCM có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔABM=ΔDCM
b: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AB//DC
c: Ta có: ΔACB cân tại A
mà AM là đường trung tuyến
nên AM là đường cao

Tham Khảo :
Bạn tự vẽ hình nha
a) Xét t/g ABM và t/g DCM có:
BM = CM (gt)
AMB = DMC ( đối đỉnh)
MA = MD (gt)
Do đó, t/g ABM = t/g DCM (c.g.c) (đpcm)
b) t/g ABM = t/g DCM (câu a)
=> ABM = DCM (2 góc tương ứng)
Mà ABM và DCM là 2 góc ở vj trí so le trong nên AB // DC (đpcm)
c) t/g AMC = t/g AMB (c.c.c)
=> AMC = AMB (2 góc tương ứng)
Mà AMC + AMB = 180o ( kề bù)
=> AMC = AMB = 90o
=> AM _|_ BC (đpcm)
d) AB // CD => BAD = ADC = 30o (so le trong)
Mà BAD = CAD do t/g AMB = t/g AMC (câu c)
=> BAD + CAD = 2.BAD = 2.30o = 60o
T/g ABC cân tại A, có BAC = 60o
=> t/g BAC đều

