Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1. Vì AB=AH(gt)
AH=AI(gt)
=> AB+AI( áp dụng tính chất bắc cầu
2. Dễ thấy góc BAH=góc BCA vì cả hai góc cùng phụ với góc ABC:
góc BAH+gócHBA=90 độ (tam giác ABH vuông tại H)
góc BCA = góc ABC = 90 độ ( tam giác ABC vuông tại A)

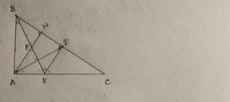
a: Xét ΔBAK có BA=BK
nên ΔBAK cân tại B
b: góc BAH+góc B=90 độ
góc ACB+góc B=90 độ
=>góc BAH=góc ACB
góc HAK+góc BKA=90 độ
góc KAI+góc BAK=90 độ
mà góc BKA=góc BAK
nên góc HAK=góc KAI
d: (AH+BC)^2=AH^2+2*AH*BC+BC^2
=AH^2+2*AB*AC+AB^2+AC^2
=AH^2+(AB+AC)^2>(AB+AC)^2
=>AH+BC>AB+AC
c: AH+BC>AB+AC
=>BC-AB>AC-AH

Vẽ nháp bằng tay, hình không đẹp cho lắm :v Bài viết có hơi lỗi.
Bài toán phụ : Chứng minh tam giác vuông có 1 góc 60 độ thì cạnh góc vuông nhỏ hơn sẽ bằng 1 nửa cạnh huyền.
Tam giác MNP vuông tại M có góc N là 60 độ.

Trên tia đối tia MN lấy điểm Q sao cho MQ=MN
Tam giác NPQ có PM vừa là trung tuyến vừa là đường cao nên cân tại P, mà lại có 1 góc 60 độ nên là tam giác đều ( Dấu hiệu nhận biết tam giác đều), từ đó suy ra NQ = NP, mà NQ= 2MN nên MN = \(\frac{1}{2}\)NP, bài toán được chứng minh.
Tương tự với bài toán của chúng ta :

\(\Delta ABC\)vuông tại Acó \(\widehat{B}=60^o\) \(\Rightarrow AB=\frac{1}{2}BC\)
\(\Delta ABH\)vuông tại H có \(\widehat{B}=60^o\) \(\Rightarrow HB=\frac{1}{2}AB\)
\(\Rightarrow HB=\frac{1}{4}BC\)
Trước hết \(\Delta ABH\) vuông tại H có \(\widehat{B}=60^o\)
nên \(\widehat{HAB}=90^o-60^o=30^o\)Mà \(\widehat{DAH}+\widehat{HAB}=\widehat{BAC}=90^o\)
\(\Rightarrow\widehat{DAH}=60^o\)
\(\Delta DAH\)cân tại A ( AD = AH ), có góc DAH là 60o nên là tam giác đều ( Dấu hiệu nhận biết tam giác đều )
Như vậy AI là đường cao đồng thời cũng là phân giác góc DAH
\(\Rightarrow\widehat{IAH}=\frac{1}{2}\widehat{DAH}=\frac{60^o}{2}=30^o\)
\(\Rightarrow\widehat{KAB}=\widehat{IAH}+\widehat{HAB}=30^o+30^o=60^o\)
\(\Delta KAB\)có \(\widehat{KAB}=\widehat{KBA}=60^o\) nên là tam giác đều
\(\Rightarrow KB=AB\)
Mà \(HB=\frac{1}{2}AB\Rightarrow HB=\frac{1}{2}KB\), hay H là trung điểm của KB.
Vậy ....
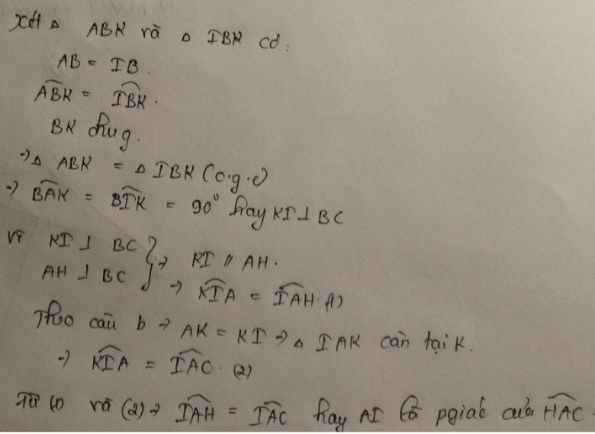
Xét tam giác ABH vuông tại H, ta có: \(\widehat{BAH}=90-\widehat{ABC}\)
Xét tam giác ABC vuông tại A, ta có: \(\widehat{ACB}=90-\widehat{ABC}\)
Từ hai điều trên suy ra: \(\widehat{BAH}=\widehat{ACB}\)
uuuuuuuuuuursasssssssssssssssss