DP
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TT
1
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
10 tháng 4 2021
Từ M kẻ \(MH\perp AC\) (H thuộc AC) ta có
\(MH\perp AC\)
\(AB\perp AC\)
=> MH//AB (cùng vuông góc với AC) (1)
BM=CM (2)
=> AH=CH (trong tam giác đường thẳng // với 1 cạnh và đi qua trung điểm của 1 cạnh thì đi qua trung điểm cạnh còn lại)
Trong ta giác AMC có
\(MH\perp AC;AH=HC\) => tam giác AMC cân tại M (ta giác có đường cao đồng thời là đường trung tuyến thì tg đó là tg cân)
=> AM=CM mà CM=BM => AM=BM=CM \(\Rightarrow AM=\frac{1}{2}BC\)
8 tháng 8 2016
a) Xét ΔABM và ΔDCM có:
BM=MC(gt)
\(\widehat{BMA}=\widehat{CMD}\)(đđ)
AM=DM
=> ΔABM=ΔDCM(c.g.c)
=>\(\widehat{ABM}=\widehat{MCD}\) .Mà 2 góc này ở vị trí soletrong)
=>AB//CD
b)Vì ΔABC vuông tại A(gt)
=> AM=BM=MC
Có: AD=AM+MD
BC=MB+MC
Mà: AM=BM(cmt); MD=MC(cmt)
=>BC=AM
Vì ΔABM=ΔDCM(cmt)
=>AB=DC
Xét ΔABC và ΔCDA có:
AB=DC(cmt)
AC: cạnh chung
BC=AD(cmt)
=>ΔABC=ΔCDM(c.c.c)
c) Vì ΔABC vuông tại A(gt)
=>AM=BC/2
S
4 tháng 3 2023
câu 2 :
a) có phải là chứng minh AM ⊥ BC không
xét ΔAMB và ΔAMC, ta có :
AB = AC (2 cạnh bên của ΔABC cân tại A)
MB = MC (AM là đường trung tuyến của cạnh BC)
AM là cạnh chung
=> ΔAMB = ΔAMC (c.c.c)
=> \(\widehat{AMB}=\widehat{AMC}\) (2 cạnh tương ứng)
mà \(\widehat{AMB}+\widehat{AMC}=180^O\) (kề bù)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}=\dfrac{180^O}{2}=90^O\)
=> AM ⊥ BC
18 tháng 8 2017
a/ Xét tam giác AMC và tam giác BMD : AM = MD (gt) ;\(\widehat{AMC}\)= \(\widehat{DMB}\) (đối đỉnh) ; BM = BC (vì là tđ BC)
\(\Rightarrow\) Tam giác AMC = tam gaics DMB (c-g-c)
b/ Ta có : \(\widehat{MBD}\)= \(\widehat{MCA}\)(câu a/) và \(\widehat{ABC}\)+ \(\widehat{ABC}\)\(=\) 90 độ (do tam giác ABC vuông)\(\Rightarrow\) \(\widehat{ABC}\)+ \(\widehat{MBD}\)
\(=\)90 độ hay \(\widehat{ABD}\)\(=\)90 độ
c/Vì AM là đường trung tuyến của BC trong tam giác vuông ABC(gt) \(\Rightarrow\)AM \(=\)1/2BC
28 tháng 7 2023
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
=>ΔABM=ΔACM
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vuông gócBC
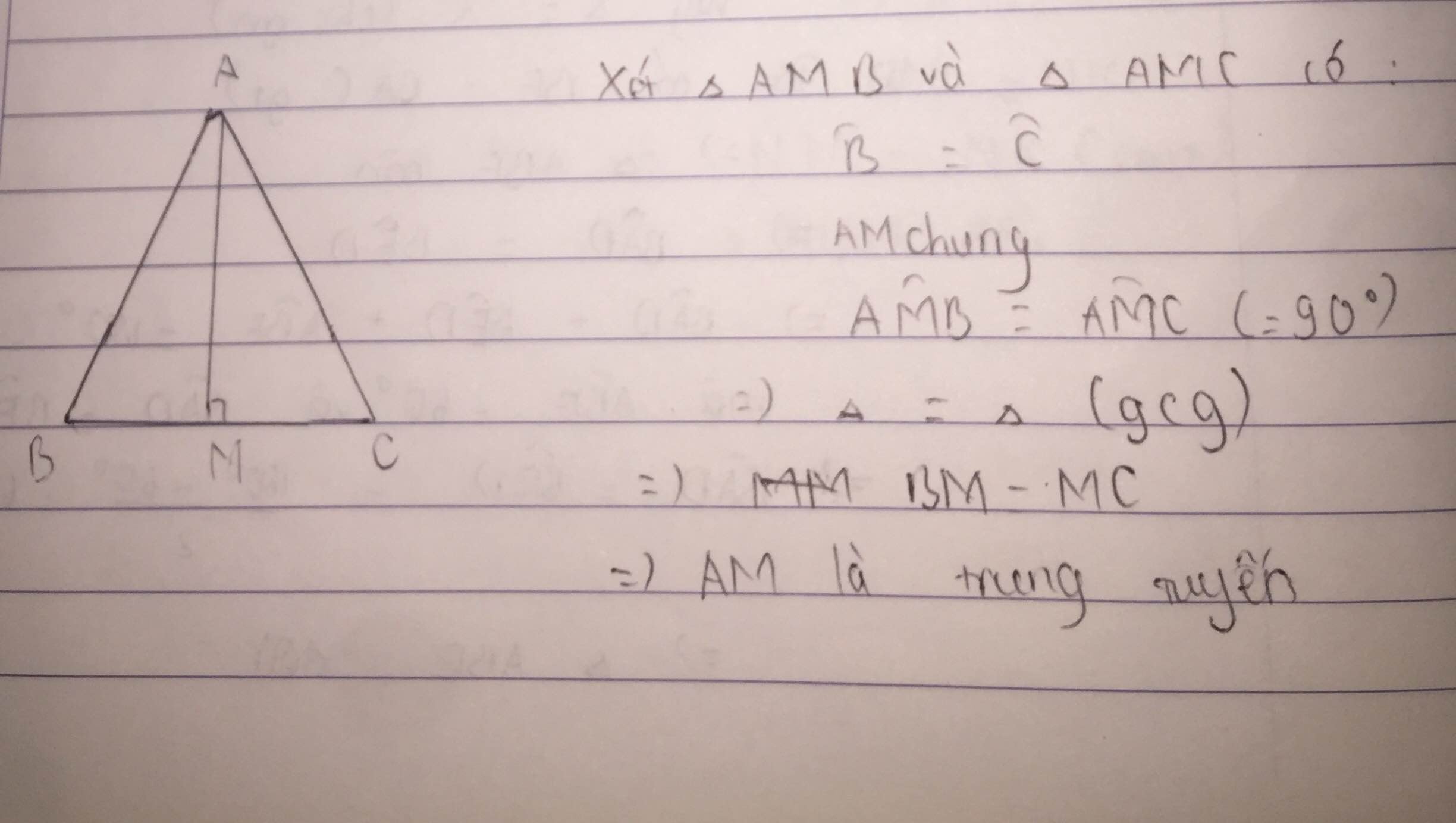
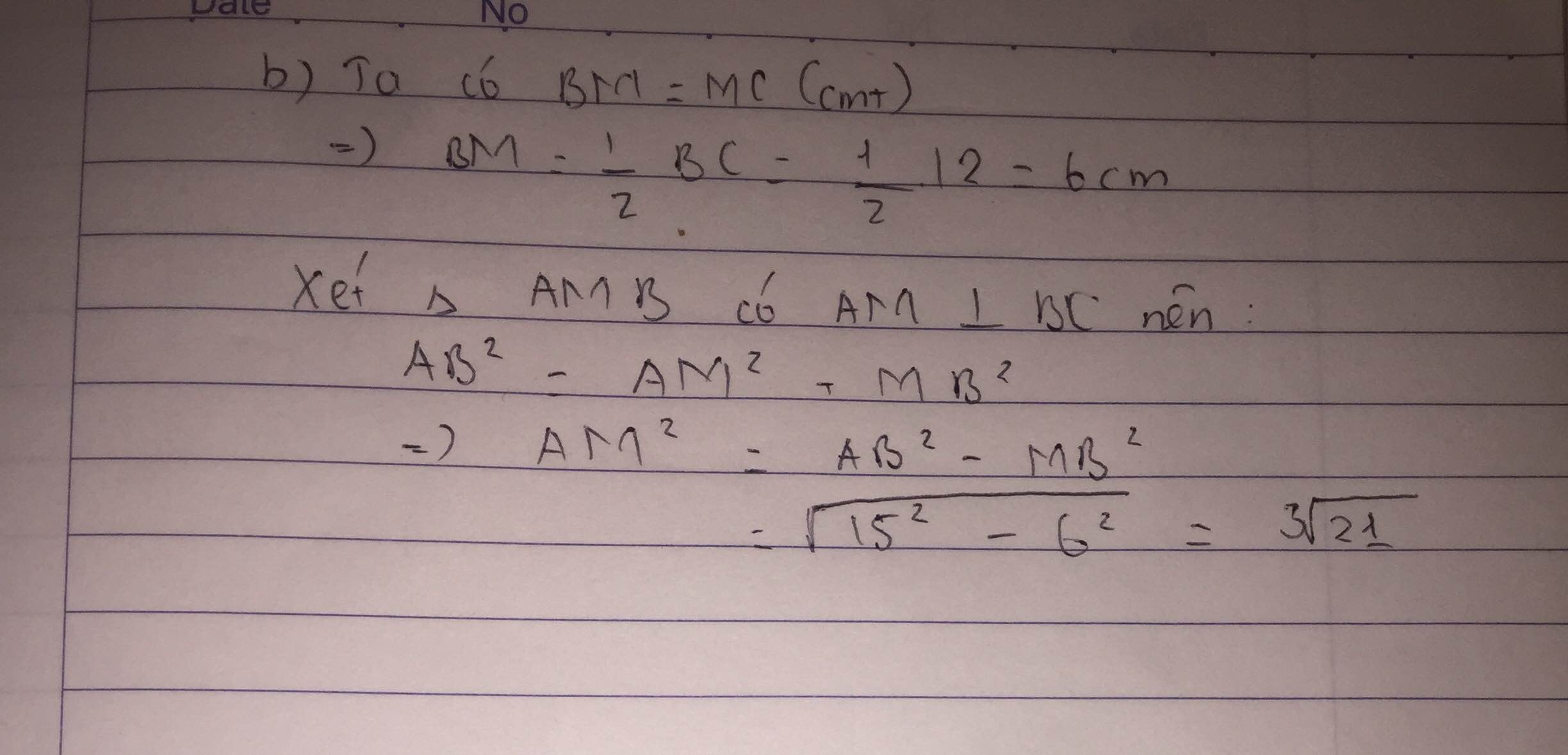
(Bạn tự vẽ hình)
Trong tam giác vuông đường trung tuyến ứng với cạnh huyền = 1/2 cạnh huyền
=> đpcm