Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. Xét tam giác ABM và tam giác DBM :
BM chung
Góc ABM =góc DBM ( gt)
BD = BA (gt)
=> Tam giác ABM = tam giác DBM ( ch-gn)
b) Ta có tam giác ABM = tam giác DBM
=> Góc BAM = góc BDM ( = 90 độ)
=> MD vuông góc với BC
c) Xét tam giác vuông DMC vuông tại D ta có :
MC > MD ( vì MC là cạnh huyền )
Mà MD = MA
=> MC > MA

a: Xét ΔBAM và ΔBDM có
BA=BD
\(\widehat{ABM}=\widehat{DBM}\)
BM chung
Do đó; ΔBAM=ΔBDM
b: Ta có: ΔBAM=ΔBDM
nên \(\widehat{BAM}=\widehat{BDM}=90^0\)
hay MD\(\perp\)BC
c: Ta có: MA=MD
mà MD<MC
nên MA<MC

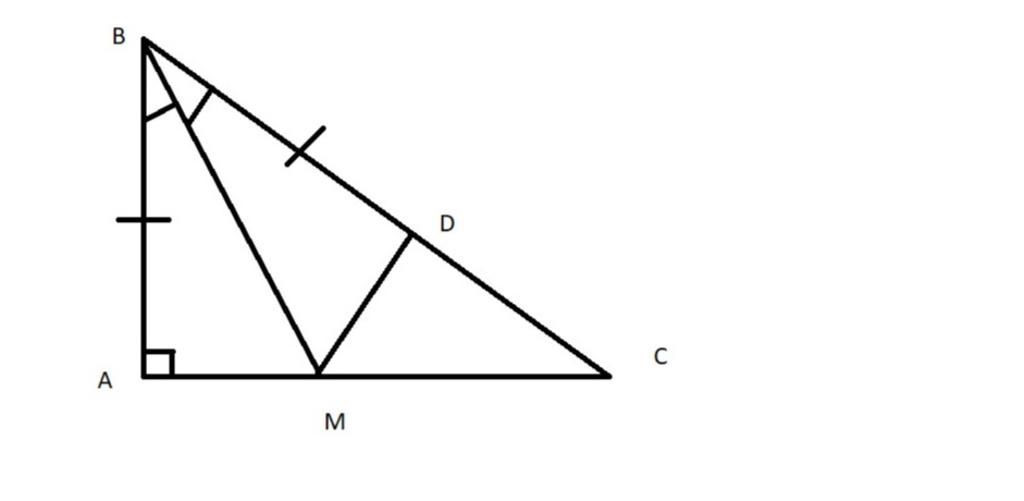

a)Xét △ABM và △△ DBM , ta có :
AB=BD(gt)
ˆABM^ == ˆDBM^ ( vì BM là tia phân giác của ˆABC^ )
BM là chung
⇒ △△ ABM= △△ DBM(c−g−c)
b)Ta có : ˆBAM^ == ˆBDM (( vì △ ABM= △ DBM)
Mà ˆBAM^ =90o(=90) ( vì △ ABC vuông tại A)
⇒⇒ ˆBDM=90o
⇒MD⇒ ⊥⊥ BC
c) Vì MD⊥⊥ BC(cmt)
⇒ ˆMDC^ =90o=90
⇒ △ MDC vuông tại D
⇒MC>MD(ch>cgv)
Mà MD=MA( vì △ABM=△ DBM)
⇒MC>MA

a) Xét ΔABM và ΔDBM có
BA=BD(gt)
\(\widehat{ABM}=\widehat{DBM}\)(BM là tia phân giác của \(\widehat{ABD}\))
BM chung
Do đó: ΔABM=ΔDBM(c-g-c)
Suy ra: \(\widehat{BAM}=\widehat{BDM}\)(hai góc tương ứng)
mà \(\widehat{BAM}=90^0\)(ΔABC vuông tại A)
nên \(\widehat{BDM}=90^0\)(đpcm)
b) Xét ΔABC vuông tại A có BC là cạnh huyền(BC là cạnh đối diện với \(\widehat{BAC}=90^0\))
nên BC là cạnh lớn nhất trong ΔABC(Định lí tam giác vuông)
Suy ra: BC>AC

a. Xét tam giác vuông ABC
Theo định lý Py - ta - go ta có :
AB2 + AC2 = BC2
=> 32 + AC2 = 52
=> 9 + AC2 = 25
=> AC2 = 16
=> AC = 4
Vậy AB < AC < BC
b. Xét tam giác BAM và tam giác BDM ta có :
BM chung
Góc BAM = góc BDM ( = 90 độ )
BA = BD ( gt)
=> tam giác BAM = tam giác BDM ( ch - cgv)
=> MA = MD ( hai cạnh tương ứng )
Xét tam giác AMN và tam giác DMC
góc AMN = góc DMC ( đối đỉnh )
MA = MD ( cmt)
góc MAN= góc MDC ( = 90 độ )
=> Tam giác AMN = tam giác DMC
=> MN = MC
=> Tam giác MNC cân

a: AC=4cm
b: Xét ΔABC có AB<AC<BC
nên \(\widehat{C}< \widehat{B}< \widehat{A}\)
c: Xét ΔBAM vuông tại A và ΔBDM vuông tại D có
BM chung
BA=BD
Do đó: ΔBAM=ΔBDM
Suy ra: MA=MD
Xét ΔAMN vuông tại A và ΔDMC vuông tại D có
MA=MD
\(\widehat{AMN}=\widehat{DMC}\)
Do đó: ΔAMN=ΔDMC
Suy ra: MN=MC
hay ΔMNC cân tại M

a,VÌ cạnh BC là cạnh huyền(BC đối góc Vuông BAC)
Áp dụng Pytago ta đc:
AB2+AC2=BC2(Pytago)
=>BC2=62+82
=>BC2=36+64=100
=>BC2=102
=>BC=10
Chúc bạn học tốt!

a: Xét ΔABM và ΔDBM có
BA=BD
\(\widehat{ABM}=\widehat{DBM}\)
BM chung
Do đó: ΔABM=ΔDBM
b: Ta có: ΔBAM=ΔBDM
nên \(\widehat{BAM}=\widehat{BDM}=90^0\)
hay MD\(\perp\)BC
c: Ta có: MA=MD
mà MD<MC
nên MA<MC