Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Vì BD là tia phân giác của góc B suy ra:
góc ABD=góc EBD
Xét tam giác ABD và tam giác EBD có:
BA=BD(gt)
góc ABD=góc EBD(cmt)
BD chung
suy ra: tam giác ABD= tam giác EBD(cgc)
Vậy tam giác ABD= tam giác EBD
b,Vì tam giác ABD=tam giác EBD nên
góc BAD=góc BED(2 góc tương ứng)
mà góc BAD=90độ(tam giác ABC vuông tại A)
suy ra góc BED=90 độ
suy ra:DE vuông góc với BC
Câu c hình như đề bài sai

a) Xét tam giác ABD và EBD CÓ
BD chung, góc abd= góc ebd, BE=BA
do dố tam giác abd= tam giác ebd (c-g-c)
b) vì tam giác ABD= tam giác EBD do đó
góc A= góc E (2 góc tương ứng)
mà góc A=90 nên góc E=90
=>DE vuông góc BC
c) Xét tam giác ADF và tam giác EDC có
AD=DE (TAM GIÁC ABD= EBD), GÓC A=GÓC E=90, HAI GÓC D BẰNG NHAU VÌ ĐỐI ĐỈNH
DO ĐÓ TAM GIÁC ADF= TAM GIÁC EDC
=>DF=DC (2 CẠNH TƯƠNG ỨNG )
MÌNH ĐÁNH CAPSLOCK THÔNG CẢM

a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
b: Ta có: ΔABD=ΔEBD
nên \(\widehat{BAD}=\widehat{BED}=90^0\)
hay DE\(\perp\)BC
c: Xét ΔADK vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)
Do đó: ΔADK=ΔEDC
Suy ra: AK=EC
Ta có: BA+AK=BK
BE+EC=BC
mà BA=BE
và AK=EC
nên BK=BC

a: Xét ΔABD và ΔEBD có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔABD=ΔEBD
b: Ta có: ΔABD=ΔEBD
nên DA=DE
Ta có: ΔABD=ΔEBD
nên \(\widehat{BAD}=\widehat{BED}=90^0\)
hay DE⊥BC

Ta có hình vẽ:
A B C D E H
a) Vì AD là phân giác của ABC nên ABD = DBC
Xét Δ ABD và Δ EBD có:
AB = BE (gt)
ABD = EBD (cmt)
BD là cạnh chung
Do đó, Δ ABD = Δ EBD (c.g.c) (đpcm)
b) Δ ABD = Δ EBD (câu a) => BAD = BED = 90o (2 góc tương ứng)
\(\Rightarrow DE\perp BE\) hay \(DE\perp BC\left(đpcm\right)\)
c) Gọi H là giao điểm của AE và BD
Xét Δ ABH và Δ EBH có:
AB = EB (gt)
ABH = EBH (câu a)
BH là cạnh chung
Do đó, Δ ABH = Δ EBH (c.g.c)
=> AH = EH (2 cạnh tương ứng) (1)
và AHB = EHB (2 góc tương ứng)
Mà AHB + EHB = 180o (kề bù) nên AHB = EHB = 90o
\(\Rightarrow BH\perp AE\) hay \(BD\perp AE\left(2\right)\)
Từ (1) và (2) => BD là đường trung trực của AE (đpcm)
Ta có hình vẽ:
A D B C E
Gọi BD cắt AE tại M
a/ Xét tam giác ABD và tam giác EBD có:
BD: cạnh chung
BA = BE (GT)
\(\widehat{ABD}\)=\(\widehat{DBE}\) (GT)
=> tam giác ABD = tam giác EBD (c.g.c)
b/ Ta có: tam giác ABD = tam giác EBD (câu a)
=> \(\widehat{A}\)=\(\widehat{E}\)=900 (2 góc tương ứng)
=> DE \(\perp\)BC (đpcm)
c/ Xét tam giác ABM và tam giác EBM có:
BM: cạnh chung
\(\widehat{ABM}\)=\(\widehat{MBE}\)(GT)
\(\widehat{A}\)=\(\widehat{E}\)=900
Trường hợp cạnh huyền góc nhọn
=> tam giác ABM = tam giác EBM (g.c.g)
=> \(\widehat{AMB}\)=\(\widehat{EMB}\) (2 góc tương ứng)
Mà \(\widehat{AMB}\)+\(\widehat{EMB}\)=1800
=> \(\widehat{AMB}\)=\(\widehat{EMB}\)=900
=> BD \(\perp\)AE
Mà BM là phân giác góc B
=> BD là trung trực của AE (đpcm)

a) ta có: A + ABC + C =180° (đ/l)
=> 90° + ABC + 40° =180°
=> ABC = 180° -( 40°+ 90°)
=> ABC = 50°
Vì BD là tia phân giác góc ABC => ABD = CBD = 50° : 2 = 25°
Vậy ABD = 25°
b) xét tam giác BAD và tam giác BED có:
AB = BE ( GT )
BD chung
ABD = CBD ( GT )
=> tam giác BAD = tam giác BED ( c.g.c )
Ta có A = BED = 90° ( 2 góc t.ư)
=> DE vuông góc BC ( vì có 1 góc= 90° )
c) xét tam giác ABC và tam giác EBF có:
AB = BE ( GT )
B chung
A = E = 90°
=> tam giác ABC = tam giác EBF ( g.c.g )
d) ta có tam giác ABC = tam giác EBF ( theo c )
=> BC = BF ( 2 cạnh tương ứng)
Xét tam giác BKC và tam giác BKF có:
BC = BF ( GT )
BK chung
FBK = KBC ( GT )
=> tam giác BKC = tam giác BKF (c.g.c)
=> BKC = BKF ( 2 góc t.ư)
=> BKC + BKF = 180° ( 2 góc kề bù )
=> BKC = BKF = 180° : 2 = 90° = KFC
Vậy 3 điểm K,F,C thẳng hàng
Bn vẽ hình hộ mk nhé!
A B C D 40
a) Áp dụng tc tổng 3 góc của 1 tg ta có:
góc BAC + ACB + ABC = 180 độ
=>90 + 40 + ABC = 180
=> ABC = 50 độ
mà góc ABD = CBD = ABC : 2 = 50 : 2 = 25 độ ( BD là tia pg của ABC )
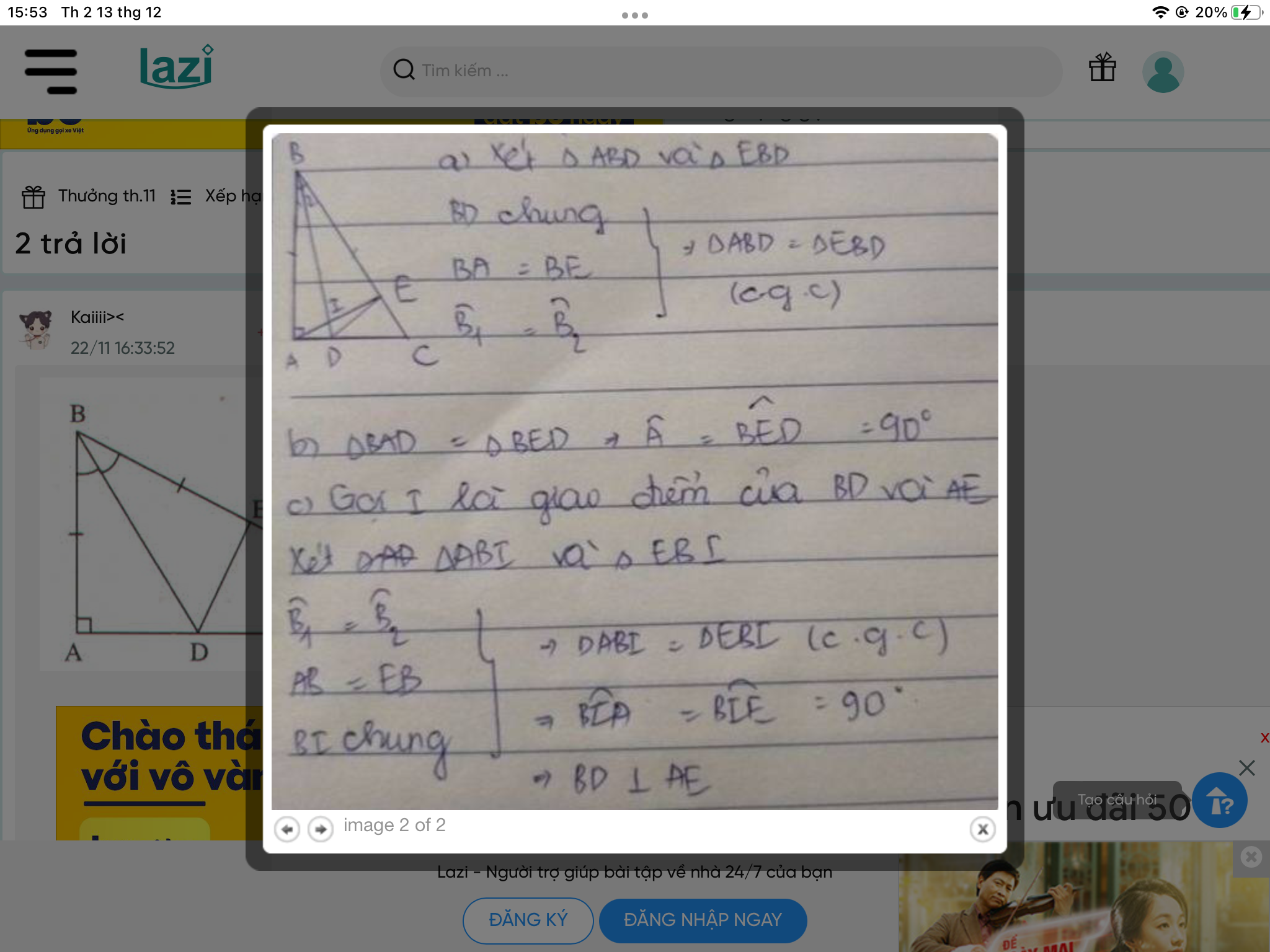
xét ΔABD và ΔEBD, có:
BA = BE (giả thiết)
\(\widehat{ABD}=\widehat{EBD}\) (giả thiết)
BD là cạnh chung
⇒ ΔABD = ΔEBD (c-g-c)
b) sao mà DE = BC được
c) vì BA = BE (giả thiết) nên ΔABE cân tại B
Lại có: BK là đường phân giác ΔABE
⇒ BK cũng là đường trung trực ΔABE
⇒ KA = KE và \(\widehat{BKE}=\widehat{BKA}=90^0\)
xét ΔDEK VÀ ΔDAK, có:
KA = KE (cmt)
\(\widehat{DKA}=\widehat{DKE}=90^0\left(cmt\right)\)
DK cạnh chung
=> ΔDEK = ΔDAK (c-g-c)