Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

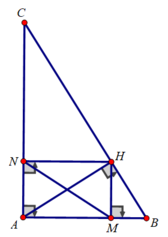
b) Xét tam giác AHB vuông tại H, HM là đường cao có:

∠(AMN) + ∠(ANM ) = 90 0 ⇒ ∠(ANM ) = 90 0 - ∠(AMN) = 53 , 1 0

c: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)


a: ΔAHB vuông tại H có HM là đường cao
nên AM*MB=HM^2
ΔAHC vuông tại H có HN là đường cao
nên AN*NC=NH^2
Xét tứ giác AMHN có
góc AMH=góc ANH=góc MAN=90 độ
=>AMHN là hình chữ nhật
=>MN^2=HM^2+HN^2
=AM*MB+AN*NC
b: ΔABC vuông tạiA có AH là đường cao
nên \(AB^2=BH\cdot BC;AC^2=CH\cdot CB\)
=>\(\dfrac{AB^2}{AC^2}=\dfrac{BH\cdot BC}{CH\cdot BC}=\dfrac{BH}{CH}\)

b: \(AN\cdot AC=AH^2\)
\(AC^2-HC^2=AH^2\)
Do đó: \(AN\cdot AC=AC^2-HC^2\)

a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
hay AH=2,4(cm)
Xét tứ giác AMHN có
\(\widehat{MAN}=\widehat{ANH}=\widehat{AMH}=90^0\)
Do đó: AMHN là hình chữ nhật
Suy ra: AH=MN=2,4(cm)
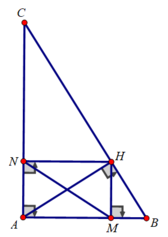
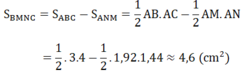
a) Xét tam giác ABC vuông tại A, đường cao AH có:
B C 2 = A B 2 + A C 2 = 25 ⇒ BC = 5(cm)
AB2 = BH.BC ⇒ BH = AB2/BC = 9/5 = 1,8(cm)
BH + CH = BC⇒ CH = BC - BH = 5 - 1,8 = 3,2 (cm)
A H 2 = BH.CH ⇒ AH = B H . C H = 1 , 8 . 3 , 2 = 2,4 (cm)
Xét tứ giác AMHN có:
∠(MAN) = ∠(ANH) = ∠(AMH) = 90 0
⇒ Tứ giác AMHN là hình chữ nhật
⇒ MN = AH = 2,4 (cm)